
 ;
;
 ,
, 为偶函数时,求
为偶函数时,求 的值。
的值。 时,
时, 在
在 上是单调递增函数,求
上是单调递增函数,求 的取值范围。
的取值范围。 时,(其中
时,(其中 ,
, ),若
),若 ,且函数
,且函数 的图像关于点
的图像关于点 对称,在
对称,在 处取得最小值,试探讨
处取得最小值,试探讨 应该满足的条件。
应该满足的条件。 ,
, ;(2)
;(2) ,
, ;
; ,
, 。
。 为偶函数,所以
为偶函数,所以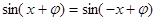 ,
,  ,
,




 ,所以
,所以 与
与 不能同时成立,
不能同时成立,  的图像关于点
的图像关于点 对称知道
对称知道 ,
, ,解得参数的值。
,解得参数的值。 为偶函数,所以
为偶函数,所以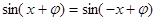 ,
, 




 2分
2分 ,
, ,
, ,
,






 4分
4分


 6分
6分 ,其中
,其中 ,所以
,所以 ,
,





 8分
8分


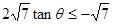 ,
, ,
, ,
,






 10分
10分






















 12分
12分 ,所以
,所以 与
与 不能同时成立,不妨设
不能同时成立,不妨设 ,
, ,
, ,其中
,其中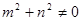 ;
; 的图像关于点
的图像关于点 对称,在
对称,在 处取得最小值,
处取得最小值, ,
, ,
,  , 所以,
, 所以, ,
,
 ①
①











 14分
14分 的图像关于点
的图像关于点 对称知道
对称知道 ,
, ,
, ,
, ,又因为
,又因为 在
在 处取得最小值,
处取得最小值, ,
, ,
,
 ②
②











 16分
16分 ,
, 。
。






 18分
18分

 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案科目:高中数学 来源:不详 题型:解答题
 ,若函数
,若函数
 ,当
,当 时,
时, 的最大值与最小值的和为2.
的最大值与最小值的和为2. 的值,并用五点法画出
的值,并用五点法画出 在长度为一个周期的区间内的简图。
在长度为一个周期的区间内的简图。 的单调区间。
的单调区间。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,
, ).
). |=|
|=| |,求角α的值;
|,求角α的值; ·
· =-1,求
=-1,求 的值.
的值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com