练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知函数

    （1）判断的奇偶性并证明；

    （2）若，求的取值范围.[来

    【答案】（1）奇函数（2）

    【解析】

    试题分析：（1）判断函数奇偶性首先判断函数定义域是否对称，再判断的关系确定奇偶性；（2）将原函数式结合复合函数单调性判定方法可得到函数单调性，进而可化简不等式得到m的不等式，可求m得取值范围

    试题解析：（1）判断：f（x）为奇函数，-----------------------1分

    证明如下：

    因为，定义域为关于原点对称---------------------3分

    -----------------6分

    （2）为上的减函数，--------------------8分

    由复合函数的单调性可知f（x）在定义域上是减函数，---------------9分

    所以有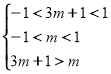解得：------------------12分

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知P＝{x|x2－8x－20≤0}，S＝{x|1－m≤x≤1＋m}.

    （1）是否存在实数m，使x∈P是x∈S的充要条件，若存在，求出m的范围；

    （2）是否存在实数m，使x∈P是x∈S的必要条件，若存在，求出m的范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中，已知点，点在直线上运动，过点与垂直的直线和线段的垂直平分线相交于点。

    （1）求动点的轨迹的方程；

    （2）过(1)中轨迹上的点作两条直线分别与轨迹相交于，两点。试探究：当直线的斜率存在且倾斜角互补时，直线的斜率是否为定值？若是，求出这个定值；若不是，说明理由。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知分别为椭圆的上、下焦点，是抛物线的焦点，点是与在第二象限的交点，且.

    （1）求椭圆的方程；

    （2）与圆相切的直线交椭圆于，若椭圆上一点满足，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知抛物线过点，且焦点为，直线与抛物线相交于两点.

    （1）求抛物线的方程，并求其准线方程；

    （2）若直线经过抛物线的焦点，当线段的长等于5时，求直线方程.

    （3）若，证明直线必过一定点，并求出该定点.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）若函数在上具有单调性，求实数的取值范围；

    （2）若在区间上，函数的图象恒在图象上方，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】“因为四边形ABCD是矩形，所以四边形ABCD的对角线相等.”补充以上推理的大前提（ ）

    A. 正方形都是对角线相等的四边形 B. 矩形都是对角线相等的四边形

    C. 等腰梯形都是对角线相等的四边形 D. 矩形都是对边平行且相等的四边形

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在一项中学生近视情况的调查中，某校男生150名中有80名近视，女生140名中有70名近视，在检验这些中学生眼睛近视是否与性别有关时用什么方法最有说服力（ ）

    A. 平均数与方差 B. 回归分析

    C. 独立性检验 D. 概率

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】假设我国发射的天宫一号飞行器需要建造隔热层.已知天宫一号建造的隔热层必须使用20年，每厘米厚的隔热层建造成本是6万元，天宫一号每年的能源消耗费用H（万元）与隔热层厚度（厘米）满足关系式：（当时表示无隔热层），若无隔热层，则每年能源消耗费用为8万元.设为隔热层建造费用与20年的能源消耗费用之和.

    （I）求的值和的表达式；

    （II）当隔热层修建多少厘米厚时，总费用最小，并求出最小值.

    查看答案和解析>>

    同步练习册答案