练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知抛物线过点，且焦点为，直线与抛物线相交于两点.

    （1）求抛物线的方程，并求其准线方程；

    （2）若直线经过抛物线的焦点，当线段的长等于5时，求直线方程.

    （3）若，证明直线必过一定点，并求出该定点.

    【答案】（1），；（2）；（3）证明见解析，.

    【解析】

    试题分析：（1）由，得，抛物线的方程为，进而求解抛物线的准线方程；（2）若直线经过焦点，则直线的方程为，即可求解和，再由，即可求解该直线方程；（3）设直线的方程为代入，得，设，则，，再利用，求得，即可判定直线过定点.

    试题解析：（1）由，得，抛物线的方程为，

    其准线方程为，焦点为.

    （2）若直线经过抛物线的焦点，则直线的方程为.

    ，，则，

    所以，得，，直线方程为.

    （3）设直线的方程为代入，得.

    设，，

    则，.

    ，

    ∴，直线必过一定点.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

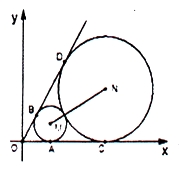
    【题目】如图，已知圆心坐标为的圆与轴及直线分别相切于、两点，另一圆与圆外切，且与轴及直线分别相切于、两点．

    （1）求圆和圆的方程；

    （2）过点作直线的平行线，求直线被圆截得的弦的长度．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】扬州瘦西湖隧道长米，设汽车通过隧道的速度为米/秒．根据安全和车流的需要，当时，相邻两车之间的安全距离为米；当时，相邻两车之间的安全距离为米（其中是常数）．当时，，当时，．

    （1）求的值；

    （2）一列由辆汽车组成的车队匀速通过该隧道（第一辆汽车车身长为米，其余汽车车身长为米，每辆汽车速度均相同）．记从第一辆汽车车头进入隧道，至第辆汽车车尾离开隧道所用的时间为秒．

    ①将表示为的函数；

    ②要使车队通过隧道的时间不超过秒，求汽车速度的范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知α、β是不同的平面，l、m、n是不同的直线，P为空间中一点．若α∩β＝l，mα、nβ、m∩n＝P，则点P与直线l的位置关系用符号表示为___.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=sin（π﹣ωx）cosωx+cos2ωx（ω＞0）的最小正周期为π．

    （Ⅰ）求ω的值；

    （Ⅱ）将函数y=f（x）的图象上各点的横坐标缩短到原来的，纵坐标不变，得到函数y=g（x）的图象，求函数y=g（x）在区间上的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数

    （1）判断的奇偶性并证明；

    （2）若，求的取值范围.[来

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】学校某研究性学习小组在对学生上课注意力集中情况的调查研究中，发现其在40分钟的一节课中，注意力指数与听课时间（单位：分钟）之间的关系满足如图所示的图象，当时，图象是二次函数图象的一部分，其中顶点，过点；当时，图象是线段，其中．根据专家研究，当注意力指数大于62时，学习效果最佳．

    （1）试求的函数关系式；

    （2）教师在什么时段内安排内核心内容，能使得学生学习效果最佳？请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数．

    （1）已知，求单调递增区间；

    （2）是否存在实数，使的最小值为0？若存在，求出的值；若不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知的三个顶点，，，其外接圆为.

    （1）求的面积；

    （2）若直线过点，且被截得的弦长为2，求直线的方程；

    （3）对于线段上的任意一点，若在以为圆心的圆上都存在不同的两点，，使得点的线段的中点，求的半径的取值范围.

    查看答案和解析>>

    同步练习册答案