Question

【题目】已知的三个顶点，，，其外接圆为.

（1）求的面积；

（2）若直线过点，且被截得的弦长为2，求直线的方程；

（3）对于线段上的任意一点，若在以为圆心的圆上都存在不同的两点，，使得点的线段的中点，求的半径的取值范围.

Answer 1

【答案】(1)；(2)或；(3).

【解析】

试题分析：(1)借助题设条件直接求解；(2)借助题设待定直线的斜率,再运用直线的点斜式方程求解；(3)借助题设建立关于的不等式,运用分析推证的方法进行求解.

试题解析：

（1）的面积为2；

（2）线段的垂直平分线方程为，线段的垂直平分线方程为，

所以外接圆圆心，半径，圆的方程为，

设圆心到直线的距离为，因为直线被圆截得的弦长为2，所以.

当直线垂直于轴时，显然符合题意，即为所求；

当直线不垂直于轴时，设直线方程为，则，解得，

综上，直线的方程为或.

（3）直线的方程为，设，，

因为点是线段的中点，所以，又，都在半径为的圆上，

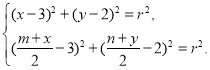所以即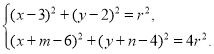

因为该关于，的方程组有解，即以为圆心，为半径的圆与以为圆心，为半径的圆有公共点，所以，

又，所以对成立.

而在上的值域为，所以且.

又线段与圆无公共点，所以对成立，即.

故圆的半径的取值范围为.