
已知数列{ }的前n项和为
}的前n项和为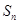 ,且
,且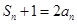 ,则使不等式
,则使不等式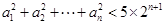 成立的n的最大值为 .
成立的n的最大值为 .
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
无穷数列 中,
中, 是首项为10,公差为
是首项为10,公差为 的等差数列;
的等差数列; 是首项为
是首项为 ,公比为
,公比为 的等比数列(其中
的等比数列(其中 ),并且对于任意的
),并且对于任意的 ,都有
,都有 成立.若
成立.若 ,则m的取值集合为____________.记数列
,则m的取值集合为____________.记数列 的前
的前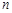 项和为
项和为 ,则使得
,则使得
 的
的 的取值集合为____________.
的取值集合为____________.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
给 个自上而下相连的正方形着黑色或白色. 当
个自上而下相连的正方形着黑色或白色. 当 时,在所有不同的着色方案中,黑色正方形互不相邻的所有着色方案如图所示. 由此推断,当
时,在所有不同的着色方案中,黑色正方形互不相邻的所有着色方案如图所示. 由此推断,当 时,黑色正方形互不相邻的着色方案共有 种,至少有两个黑色正方形相邻的着色方案共有 种. (直接用数字作答)
时,黑色正方形互不相邻的着色方案共有 种,至少有两个黑色正方形相邻的着色方案共有 种. (直接用数字作答)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com