
【题目】前些年有些地方由于受到提高![]() 的影响,部分企业只重视经济效益而没有树立环保意识,把大量的污染物排放到空中与地下,严重影响了人们的正常生活,为此政府进行强制整治,对不合格企业进行关闭,整顿,另一方面进行大量的绿化来净化和吸附污染物,通过几年的整治,环境明显得到好转,针对政府这一行为,老百姓大大点赞.
的影响,部分企业只重视经济效益而没有树立环保意识,把大量的污染物排放到空中与地下,严重影响了人们的正常生活,为此政府进行强制整治,对不合格企业进行关闭,整顿,另一方面进行大量的绿化来净化和吸附污染物,通过几年的整治,环境明显得到好转,针对政府这一行为,老百姓大大点赞.
(1)某机构随机访问50名居民,这50名居民对政府的评分(满分100分)如下表:
分数 |
|
|
|
|
|
|
频数 | 2 | 3 | 11 | 14 | 11 | 9 |
请在答题卡上作出居民对政府的评分频率分布直方图:
(2)当地环保部门随机抽测了2019年6月的空气质量指数,其数据如下表:
空气质量指数 | 0—50 | 50—100 | 100—150 | 150—200 |
天数 | 2 | 18 | 8 | 2 |
用空气质量指数的平均值作为该月空气质量指数级别,求出该月空气质量指数级别为第几级?(同一组数据用该组数据的区间中点值作代表,将频率视为概率)(相关知识参见附表)
(3)空气受到污染,呼吸系统等疾病患者最易感染,根据历史经验,凡遇到空气轻度污染,小李每天会服用有关药品花费50元,遇到中度污染每天服药的费用达到100元.环境整治前的2015年11月份小李因受到空气污染患呼吸系统等疾病花费了5000元,试估计2019年11月份(参考(2)中表格数据)小李比以前少花了多少钱的医药费?
附:
空气质量指数 | 0-50 | 50-100 | 100-150 | 150-200 | 200-300 | >300 |
空气质量指数级别 | I | II | III | IV | V | VI |
空气质量指数 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
【答案】(1)直方图见解析;(2)第Ⅱ级;(3)4400元.
【解析】
(1)计算出每组频率除以组距的值做为纵轴的数值;(2)利用组中值计算出平均值,根据表格判断空气质量指数级别为第几级;(3)根据(2)中表格数据,计算出轻度污染和重度污染对应的服药费用总和,然后和以前的费用做对比去计算少花的钱.
(1)由评分表可知,相应区间频率除以组距的值分别为0.008,0.012,0.044,0.056,0.044,0.036,其频率分布直方图如图所示:
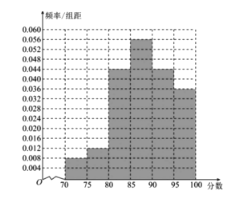
(2)由题得,该月空气质量指数平均值为![]() .
.
对照表格可知,该月空气质量指数为第Ⅱ级,属于良.
(3)估计2019年11月份轻度污染有8天,中度污染有2天,
所以小李花费的药费为![]() 元.
元.
又![]() 元,所以相比2015年11月份,
元,所以相比2015年11月份,
小李少花费了4400元的医药费.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:高中数学 来源: 题型:
【题目】如图,已知点E是圆心为O1半径为2的半圆弧上从点B数起的第一个三等分点,点F是圆心为O2半径为1的半圆弧的中点,AB、CD分别是两个半圆的直径,O1O2=2,直线O1O2与两个半圆所在的平面均垂直,直线AB、DC共面.
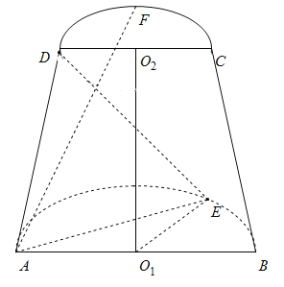
(1)求三棱锥D﹣ABE的体积;
(2)求直线DE与平面ABE所成的角的正切值;
(3)求直线AF与BE所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() ,点
,点![]() 是圆
是圆![]() 上的动点,
上的动点,![]() 为线段
为线段![]() 的中点,
的中点,![]() 为线段
为线段![]() 上点,且
上点,且![]() ,设动点
,设动点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(Ⅰ)求曲线![]() 的方程;
的方程;
(Ⅱ)直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 、
、![]() 两点,与圆
两点,与圆![]() 相交于另一点
相交于另一点![]() ,且点
,且点![]() 、
、![]() 位于点
位于点![]() 的同侧,当
的同侧,当![]() 面积最大时,求
面积最大时,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解青少年的肥胖是否与常喝碳酸饮料有关,现对30名青少年进行调查,得到如下列联表:
常喝 | 不常喝 | 总计 | |
肥胖 | 2 | ||
不肥胖 | 18 | ||
总计 | 30 |
已知从这30名青少年中随机抽取1名,抽到肥胖青少年的概率为![]() .
.
(1)请将列联表补充完整;(2)是否有99.5%的把握认为青少年的肥胖与常喝碳酸饮料有关?
独立性检验临界值表:
P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式:![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知,椭圆C过点![]() ,两个焦点为
,两个焦点为![]() ,
,![]() ,E,F是椭圆C上的两个动点,如果直线AE的斜率与AF的斜率互为相反数,直线EF的斜率为
,E,F是椭圆C上的两个动点,如果直线AE的斜率与AF的斜率互为相反数,直线EF的斜率为![]() ,直线l与椭圆C相切于点A,斜率为
,直线l与椭圆C相切于点A,斜率为![]() .
.
![]() 求椭圆C的方程;
求椭圆C的方程;
![]() 求
求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知R为圆![]() 上的一动点,R在x轴,y轴上的射影分别为点S,T,动点P满足
上的一动点,R在x轴,y轴上的射影分别为点S,T,动点P满足![]() ,记动点P的轨迹为曲线C,曲线C与x轴交于A,B两点.
,记动点P的轨迹为曲线C,曲线C与x轴交于A,B两点.
(1)求曲线C的方程;
(2)已知直线AP,BP分别交直线![]() 于点M,N,曲线C在点Р处的切线与线段MN交于点Q,求
于点M,N,曲线C在点Р处的切线与线段MN交于点Q,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点为
的左、右焦点为![]() ,点
,点![]() 在椭圆
在椭圆![]() 上.
上.
(1)设点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,证明:
,证明:![]() 为定值;
为定值;
(2)若![]() 是椭圆
是椭圆![]() 上的两个动点(都不与
上的两个动点(都不与![]() 重合),直线
重合),直线![]() 的斜率互为相反数,求直线
的斜率互为相反数,求直线![]() 的斜率(结果用
的斜率(结果用![]() 表示)
表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com