
分析 (I)由6Sn=an2+3an+2,当n≥2时,$6{S}_{n-1}={a}_{n-1}^{2}+3{a}_{n-1}$+2,可得:6an=${a}_{n}^{2}$-${a}_{n-1}^{2}$+3an-3an-1,化为(an+an-1)(an-an-1-3)=0,根据数列{an}是正项数列,及其等差数列的通项公式、a2是a1和a6的等比中项即可得出.
(II)${b_n}=[{log_2}\frac{{{a_n}+5}}{3}]$=[log2(n+1)],可得${b}_{{2}^{n}}$=$[lo{g}_{2}({2}^{n}+1)]$=n,${2}^{n}•{b}_{{2}^{n}}$=n•2n.利用“错位相减法”与等比数列的前n项和公式即可得出.
解答 解:(I)由6Sn=an2+3an+2,当n≥2时,$6{S}_{n-1}={a}_{n-1}^{2}+3{a}_{n-1}$+2,可得:6an=${a}_{n}^{2}$-${a}_{n-1}^{2}$+3an-3an-1,
化为(an+an-1)(an-an-1-3)=0,
∵数列{an}是正项数列,∴an+an-1>0,可得an-an-1=3,
∴数列{an}是等差数列,公差为3.
由6a1=${a}_{1}^{2}$+3a1+2,解得a1=1或2.
当a1=2时,an=2+3(n-1)=3n-1,可得a2=5,a6=17,不满足a2是a1和a6的等比中项,舍去.
当a1=1时,an=1+3(n-1)=3n-2,可得a2=4,a6=16,满足a2是a1和a6的等比中项.
∴an=3n-2.
(II)${b_n}=[{log_2}\frac{{{a_n}+5}}{3}]$=[log2(n+1)],∴${b}_{{2}^{n}}$=$[lo{g}_{2}({2}^{n}+1)]$=n,
∴${2}^{n}•{b}_{{2}^{n}}$=n•2n.
∴数列$\{{2^n}•{b_{2^n}}\}$的前n项和Tn=2+2×22+3×23+…+n•2n,
2Tn=22+2×23+…+(n-1)•2n+n•2n+1,
∴-Tn=2+22+…+2n-n•2n+1=2×$\frac{{2}^{n}-1}{2-1}$-n•2n+1=(1-n)•2n+1-2,
∴Tn=(n-1)•2n+1+2.
点评 本题考查了等差数列与等比数列的通项公式及其前n项和公式、“错位相减法”,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {e,lne} | B. | {e} | C. | {e,lne2} | D. | {lne,lne2} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 16 | 17 | 18 | 19 |
| y | 50 | 34 | 41 | 31 |
| A. | 26个 | B. | 27个 | C. | 28个 | D. | 29个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
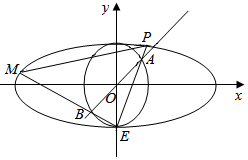 如图,椭圆C1:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\;(a>b>0)$和圆C2:x2+y2=b2,已知圆C2将椭圆C1的长轴三等分,且圆C2的面积为π.椭圆C1的下顶点为E,过坐标原点O且与坐标轴不重合的任意直线l与圆C2相交于点A,B,直线EA,EB与椭圆C1的另一个交点分别是点P,M.
如图,椭圆C1:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\;(a>b>0)$和圆C2:x2+y2=b2,已知圆C2将椭圆C1的长轴三等分,且圆C2的面积为π.椭圆C1的下顶点为E,过坐标原点O且与坐标轴不重合的任意直线l与圆C2相交于点A,B,直线EA,EB与椭圆C1的另一个交点分别是点P,M.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com