
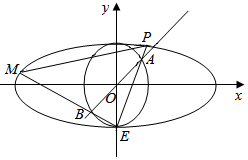
 如图,椭圆C1:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\;(a>b>0)$和圆C2:x2+y2=b2,已知圆C2将椭圆C1的长轴三等分,且圆C2的面积为π.椭圆C1的下顶点为E,过坐标原点O且与坐标轴不重合的任意直线l与圆C2相交于点A,B,直线EA,EB与椭圆C1的另一个交点分别是点P,M.
如图,椭圆C1:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\;(a>b>0)$和圆C2:x2+y2=b2,已知圆C2将椭圆C1的长轴三等分,且圆C2的面积为π.椭圆C1的下顶点为E,过坐标原点O且与坐标轴不重合的任意直线l与圆C2相交于点A,B,直线EA,EB与椭圆C1的另一个交点分别是点P,M.分析 (Ⅰ)由圆的面积公式可得b=1,再由三等分可得a=3b=3,进而得到椭圆方程;
(Ⅱ)由题意得:直线PE,ME的斜率存在且不为0,PE⊥EM,不妨设直线PE的斜率为k(k>0),则PE:y=kx-1,
代入椭圆方程求得P,M的坐标,再由直线和圆方程联立,求得A的坐标,直线AB的斜率,求得△EPM的面积,化简整理,运用基本不等式可得最大值,进而得到所求直线的斜率,可得直线方程.
解答 解:(Ⅰ)由圆C2的面积为π,得:b=1,
圆C2将椭圆C1的长轴三等分,可得a=3b=3,
所以椭圆方程为:$\frac{{x}^{2}}{9}$+y2=1;
(Ⅱ)由题意得:直线PE,ME的斜率存在且不为0,PE⊥EM,
不妨设直线PE的斜率为k(k>0),则PE:y=kx-1,
由$\left\{\begin{array}{l}{y=kx-1}\\{{x}^{2}+9{y}^{2}=9}\end{array}\right.$,得:$\left\{\begin{array}{l}{x=\frac{18k}{1+9{k}^{2}}}\\{y=\frac{9{k}^{2}-1}{9{k}^{2}+1}}\end{array}\right.$或$\left\{\begin{array}{l}{x=0}\\{y=1}\end{array}\right.$,
所以P($\frac{18k}{9{k}^{2}+1}$,$\frac{9{k}^{2}-1}{9{k}^{2}+1}$),同理得M($\frac{-18k}{{k}^{2}+9}$,$\frac{9-{k}^{2}}{9+{k}^{2}}$),
kPM=$\frac{{k}^{2}-1}{10k}$,
由$\left\{\begin{array}{l}{y=kx-1}\\{{x}^{2}+{y}^{2}=1}\end{array}\right.$,得A($\frac{2k}{1+{k}^{2}}$,$\frac{{k}^{2}-1}{{k}^{2}+1}$),所以:kAB=$\frac{{k}^{2}-1}{2k}$,
所以${S_{△EPM}}=\frac{1}{2}|{PE}|•|{EM}|=\frac{{162(k+{k^3})}}{{9{k^4}+82{k^2}+9}}=\frac{{162(k+\frac{1}{k})}}{{9{k^2}+82+\frac{9}{k^2}}}$,
设$t=k+\frac{1}{k}$,则${S_{△EPM}}=\frac{162t}{{9{t^2}+64}}=\frac{162}{{9{t^{\;}}+\frac{64}{t}}}≤\frac{27}{8}$,
当且仅当$t=k+\frac{1}{k}=\frac{8}{3}$时取等号,所以k-$\frac{1}{k}$=±$\frac{2}{3}$$\sqrt{7}$,
则直线AB:y=$\frac{{k}^{2}-1}{2k}$x=$\frac{1}{2}$(k-$\frac{1}{k}$)x,
所以所求直线l方程为:$y=±\frac{{\sqrt{7}}}{3}x$.
点评 本题考查椭圆方程的求法,注意运用圆的面积和三等分思想,考查直线方程的求法,注意运用直线方程和椭圆方程联立,以及直线和圆方程联立,求得交点,以及直线的斜率,运用基本不等式,考查化简整理的运算能力,属于中档题.


 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}}{144}$+$\frac{{y}^{2}}{108}$=1 | B. | $\frac{{x}^{2}}{36}$+$\frac{{y}^{2}}{32}$=1 | C. | $\frac{{x}^{2}}{32}$+$\frac{{y}^{2}}{36}$=1 | D. | $\frac{{x}^{2}}{36}$+$\frac{{y}^{2}}{27}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {0,1,2} | B. | {0,1,} | C. | {0,3,4} | D. | {3,4} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | |x+4| | B. | |2-x| | C. | 2+|x+1| | D. | 3-|x+1| |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
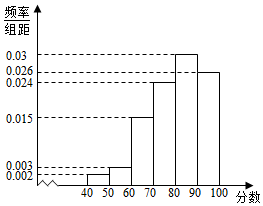 作为市政府为民办实事之一的公共自行车建设工作已经基本完成了,相关部门准备对该项目进行验收,验收的硬性指标是:市民对该项目的满意指数不低于0.8,否则该项目需进行整改,该部门为了了解市民对该项目的满意程度,在公共自行车自助点随机访问了前来使用的100名市民,并根据这100名市民对该项目满意程度的评分(满分100分),绘制了如图频率分布直方图:
作为市政府为民办实事之一的公共自行车建设工作已经基本完成了,相关部门准备对该项目进行验收,验收的硬性指标是:市民对该项目的满意指数不低于0.8,否则该项目需进行整改,该部门为了了解市民对该项目的满意程度,在公共自行车自助点随机访问了前来使用的100名市民,并根据这100名市民对该项目满意程度的评分(满分100分),绘制了如图频率分布直方图:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com