
���� ��1��ʹ�üӼ���Ԫ����ͬ�����Ǻ����Ĺ�ϵ�������õ���ͨ���̣�
��2����ֱ�ߵIJ������̴���Բ����ͨ���̣����ݲ����ļ����������ϵ���Ĺ�ϵ�����
��� �⣺��1��ֱ��l����ͨ����Ϊx-$\sqrt{3}y$-1=0��
ԲC����ͨ����Ϊ��x-2��2+y2=9��
��2����$\left\{\begin{array}{l}{x=1+\frac{\sqrt{3}}{2}t}\\{y=\frac{1}{2}t}\end{array}\right.$���루x-2��2+y2=9��t2-$\sqrt{3}t$-8=0��
��t1+t2=$\sqrt{3}$��t1t2=-8��
��|FA|+|FB|=|t1-t2|=$\sqrt{��{t}_{1}+{t}_{2}��^{2}-4{t}_{1}{t}_{2}}$=$\sqrt{35}$��
���� ���⿼���˲�����������ͨ���̵�ת���������ļ��������Ӧ�ã����ڻ����⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
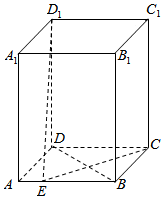 ��ͼ����������ABCD-A1B1C1D1�У�����ABCD�������Σ�����AA1�͵���ABCD����֪AB=1��${A}{{A}_1}=\sqrt{3}$��EΪAB��һ�����㣬��D1E+CE����СֵΪ��������
��ͼ����������ABCD-A1B1C1D1�У�����ABCD�������Σ�����AA1�͵���ABCD����֪AB=1��${A}{{A}_1}=\sqrt{3}$��EΪAB��һ�����㣬��D1E+CE����СֵΪ��������| A�� | $2\sqrt{2}$ | B�� | $\sqrt{10}$ | C�� | $\sqrt{5}+1$ | D�� | $2+\sqrt{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{4}$ | B�� | $\frac{1}{2}$ | C�� | 1 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ij�������ŶԸ������ij�����4�괺���ڼ䣨ÿ���ͳ�ƴ��ڼ��ڵ�ǰ7�죩�Ŀ�����Ⱦָ��������ͳ�Ʒ������Ұ��Ƿ�ȼ�ű��ڷֳ����飬�õ���ͼ�ľ�Ҷͼ�����ݹ������±���������Ⱦָ��������100�ı�ʾû������������100�ı�ʾ��������
ij�������ŶԸ������ij�����4�괺���ڼ䣨ÿ���ͳ�ƴ��ڼ��ڵ�ǰ7�죩�Ŀ�����Ⱦָ��������ͳ�Ʒ������Ұ��Ƿ�ȼ�ű��ڷֳ����飬�õ���ͼ�ľ�Ҷͼ�����ݹ������±���������Ⱦָ��������100�ı�ʾû������������100�ı�ʾ��������| ȼ�� | δȼ�� | �ϼ� | |
| ������ | |||
| ������ | |||
| �ϼ� |
| P��K2��k�� | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��һ���� | B�� | �ڶ����� | C�� | �������� | D�� | �������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
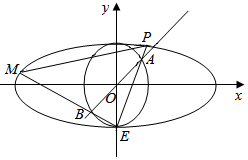 ��ͼ����ԲC1��$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\;��a��b��0��$��ԲC2��x2+y2=b2����֪ԲC2����ԲC1�ij������ȷ֣���ԲC2�����Ϊ�У���ԲC1���¶���ΪE��������ԭ��O����������غϵ�����ֱ��l��ԲC2�ཻ�ڵ�A��B��ֱ��EA��EB����ԲC1����һ������ֱ��ǵ�P��M��
��ͼ����ԲC1��$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\;��a��b��0��$��ԲC2��x2+y2=b2����֪ԲC2����ԲC1�ij������ȷ֣���ԲC2�����Ϊ�У���ԲC1���¶���ΪE��������ԭ��O����������غϵ�����ֱ��l��ԲC2�ཻ�ڵ�A��B��ֱ��EA��EB����ԲC1����һ������ֱ��ǵ�P��M���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com