
分析 (Ⅰ)由b=atanB得:bcosB=asinB,再利用正弦定理即可得出.
(Ⅱ)由(Ⅰ)知$cos2B-sinA=2{cos^2}B-cosB-1=2{(cosB-\frac{1}{4})^2}-\frac{9}{8}$,利用二次函数的单调性、三角函数的单调性与值域即可得出.
解答 解:(Ⅰ)由b=atanB得:bcosB=asinB(1分)
又由正弦定理得,sinBcosB=sinAsinB,(3分)
所以cosB=sinA(4分)
又△ABC是钝角三角形,所以$A-B=\frac{π}{2}$. (6分)
(Ⅱ)由(Ⅰ)知$cos2B-sinA=2{cos^2}B-cosB-1=2{(cosB-\frac{1}{4})^2}-\frac{9}{8}$(8分)
又由$A>\frac{π}{2}$,所以$0<B<\frac{π}{2},0<C=π-(A+B)=\frac{π}{2}-2B<\frac{π}{2}$,
所以$0<B<\frac{π}{4}$,$\frac{{\sqrt{2}}}{2}<cosB<1$(10分)
又由于函数$y=2{(x-\frac{1}{4})^2}-\frac{9}{8}$在$(\frac{{\sqrt{2}}}{2},1)$上单调递增,
所以cos2B-sinA的取值范围为$(-\frac{{\sqrt{2}}}{2},0)$.(12分)
点评 本题考查了正弦定理、二次函数的单调性、三角函数的单调性与值域,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{3}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{4}$ | D. | $\frac{2π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
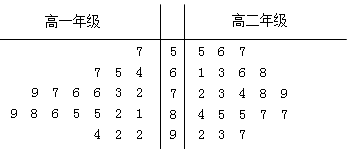
| A. | 高一学生满意度评分的平均值比高二学生满意度评分的平均值高 | |
| B. | 高一学生满意度评分比较集中,高二学生满意度评分比较分散 | |
| C. | 高一学生满意度评分的中位数为80 | |
| D. | 高二学生满意度评分的中位数为74 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 20 | B. | 120 | C. | 2400 | D. | 14400 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
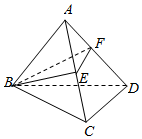 如图,在三棱锥A-BCD中,E是AC中点,F在线段AD上,且FD=3AF,则三棱锥A-BEF的体积与四棱锥B-ECDF的体积的比值为$\frac{1}{7}$.
如图,在三棱锥A-BCD中,E是AC中点,F在线段AD上,且FD=3AF,则三棱锥A-BEF的体积与四棱锥B-ECDF的体积的比值为$\frac{1}{7}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com