
���� ��1������y1��y2���Ƚϴ�Сȷ�����������ټ������۶
��2����f��x��=y1-y2����f��x����[6��14��������㣬�������Ĵ����Զ����в���ʽ����a�ķ�Χ��
��� �⣺��1����a=$\frac{1}{7}$��x=7ʱ��y1=$\frac{1}{7}$��7+$\frac{7}{2}$����$\frac{1}{7}$��2-$\frac{1}{7}$=1+$\frac{1}{14}$-$\frac{1}{7}$=$\frac{13}{14}$��
y2=-$\frac{1}{224}$����7��2-$\frac{1}{112}$��7+1=$\frac{37}{32}$��
��y1��y2��
��������۶�Ϊ7��$\frac{23}{32}$��104��50313��Ԫ����
��2����f��x��=y1-y2=$\frac{1}{224}$x2+��$\frac{1}{112}$+a��x+$\frac{7}{2}{a}^{2}$-a-1��
��f��x����[6��14��������㣬
��a��0����f��x���Գ���Ϊֱ��x=-$\frac{\frac{1}{112}+a}{\frac{1}{112}}$��0����f��x����ͼ�����ϣ�
��f��x����[6��14����ֻ��1����㣬
��$\left\{\begin{array}{l}{f��6����0}\\{f��14����0}\end{array}\right.$����$\left\{\begin{array}{l}{\frac{36}{224}+6��\frac{1}{112}+a��+\frac{7}{2}{a}^{2}-a-1��0}\\{\frac{196}{224}+14��\frac{1}{112}+a��+\frac{7}{2}{a}^{2}-a-a��0}\end{array}\right.$��
��a��0��
��ã�0��a��$\frac{1}{7}$��
���� ���⿼���˶��κ��������ʣ����Ĵ����Զ����������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
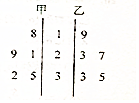 �ס����������ݵľ�Ҷͼ��ͼ��ʾ����ƽ������С��һ����Ϊ�ף���ѡ��ס����ҡ���
�ס����������ݵľ�Ҷͼ��ͼ��ʾ����ƽ������С��һ����Ϊ�ף���ѡ��ס����ҡ����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| X | 3 | 4 | 5 | 6 |
| Y | 25 | 30 | 40 | 45 |
| A�� | 59.5 | B�� | 52.5 | C�� | 56 | D�� | 63.5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | $\sqrt{3}$ | C�� | 2 | D�� | -2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 12��ѡ�� | B�� | 14��ѡ�� | C�� | 24��ѡ�� | D�� | 22��ѡ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{2}$ | B�� | $\sqrt{3}$ | C�� | $\frac{2\sqrt{3}}{3}$ | D�� | 2$\sqrt{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com