
 满足:①定义域为
满足:①定义域为 ;②对任意
;②对任意 ,有
,有 ;③当
;③当 时,
时, .则方程
.则方程 在区间
在区间 内的解的个数是( )
内的解的个数是( ) | A.18 | B.12 | C.11 | D.10 |


科目:高中数学 来源:不详 题型:解答题
 ,后20天价格为f(t)="45" (31£ t £50, tÎN),且销售量近似地满足g(t)=" -2t+200" (1£t£50, tÎN).
,后20天价格为f(t)="45" (31£ t £50, tÎN),且销售量近似地满足g(t)=" -2t+200" (1£t£50, tÎN).查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
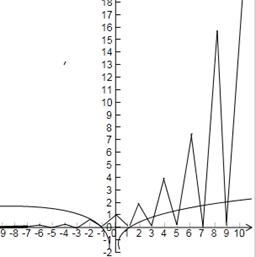
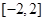 上的函数
上的函数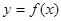 和
和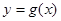 ,其图象如下图所示:
,其图象如下图所示: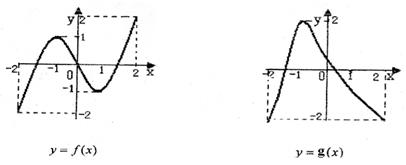
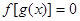 有且仅有6个根 ②方程
有且仅有6个根 ②方程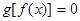 有且仅有3个根
有且仅有3个根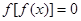 有且仅有5个根 ④方程
有且仅有5个根 ④方程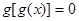 有且仅有4个根
有且仅有4个根| A.①②③ | B.②③④ | C.①②④ | D.①③④ |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.直线x=1对称 | B.点(1,1)对称 |
C.点(1,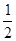 )对称 )对称 | D.点(2,1)对称 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com