
分析 ①利用函数定义域求解方法,可得结论;
②根据单调增函数的定义,即可判断;
③先在直角坐标系中分别画出函数y=-2x+2和y=-2x2+4x+2的图象,再利用函数f(x)的定义,取函数图象靠下的部分作为函数f(x)的图象,由图数形结合即可得f(x)的最大值;
④利用奇函数的定义进行判断即可.
解答 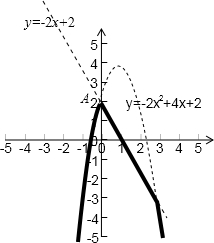 解:①若函数f(x)的定义域为[0,4],则0≤x2≤4,∴-1≤x≤2,∴函数f(x2)的定义域为[-2,2],正确;
解:①若函数f(x)的定义域为[0,4],则0≤x2≤4,∴-1≤x≤2,∴函数f(x2)的定义域为[-2,2],正确;
②若函数f(x)在区间(-∞,0)上递增,在区间[0,+∞)上也递增,则函数f(x)必在R上递增,不正确,比如在0处右边的图象在坐标图象的下方;
③如图,虚线为函数y=-2x+2和y=-2x2+4x+2的图象,粗线为f(x)的图象
由图可知函数f(x)在x=0时取得最大值2,不正确
④若函数f(x)=$\frac{{3}^{x}-{2}^{-x}}{{3}^{x}+{2}^{-x}}$,则f(-x)=-f(x),即函数f(x)在R上是奇函数,正确.
故答案为:①④.
点评 本题考查命题的真假判断,考查函数的定义域、单调性、奇偶性,函数的最值,知识综合性强.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:高中数学 来源: 题型:填空题
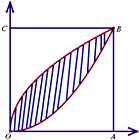 如图,在正方形OABC内,阴影部分是由两曲线y=$\sqrt{x}$,y=x2(0≤x≤1)围成,在正方形内随机取一点,且此点取自阴影部分的概率是a,则函数f(x)=$\left\{\begin{array}{l}{lo{g}_{3}x(x≥a)}\\{(\frac{1}{3})^{x}(x<a)}\end{array}\right.$的值域为[-1,+∞).
如图,在正方形OABC内,阴影部分是由两曲线y=$\sqrt{x}$,y=x2(0≤x≤1)围成,在正方形内随机取一点,且此点取自阴影部分的概率是a,则函数f(x)=$\left\{\begin{array}{l}{lo{g}_{3}x(x≥a)}\\{(\frac{1}{3})^{x}(x<a)}\end{array}\right.$的值域为[-1,+∞).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
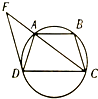 如图,已知梯形ABCD内接于圆O,AB∥CD,过点D作圆的切线交CA的延长线于点F,且DF∥BC,如果CA=5,BC=4.
如图,已知梯形ABCD内接于圆O,AB∥CD,过点D作圆的切线交CA的延长线于点F,且DF∥BC,如果CA=5,BC=4.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图所示,D是△ABC的AB边上的中点,则向量$\overrightarrow{CD}$=①(填写正确的序号).
如图所示,D是△ABC的AB边上的中点,则向量$\overrightarrow{CD}$=①(填写正确的序号).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com