
| A. | 3个 | B. | 2个 | C. | 1个 | D. | 0个 |
分析 ①根据否命题的定义进行判断,
②根据复合命题的定义进行判断,
③根据充分条件和必要条件的定义进行判断即可.
解答 解:①命题“若x=1,则x2+x-2=0”的否命题为“若x≠1,则x2+x-2≠0”;故①错误,
②设命题p:?x0∈(0,∞),log2x0<log3x0,正确,比如x0=$\frac{1}{2}$时,不等式成立,
命题q:?x∈(0,$\frac{π}{2}$),tanx>sinx等价为$\frac{sinx}{cosx}$>sinx,即$\frac{1}{cosx}$>1,
即0<cosx<1,则q为真命题.,则p∧q为真命题;故②正确,
③由ab+1>a+b得ab+1-a-b>0,
即(a-1)(b-1)>0,则a>1,b>1或a<1,b<1,则a2+b2<1不一定成立,
若a2+b2<1,则-1<a<1且-1<b<1则(a-1)(b-1)>0成立,即必要性成立,
综上可知:“ab+1>a+b”是“a2+b2<1”的必要不充分条件,故③正确,
故真命题的个数为2个,
故选:B.
点评 本题主要考查命题的真假判断,涉及四种命题的真假关系,复合命题的真假以及充分条件和必要条件的判断,综合性较强,但难度不大.


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
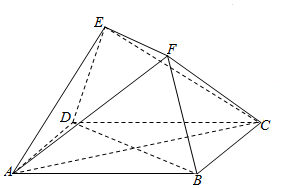 如图,多面体ABCDEF中,四边形ABCD是边长为2的正方形,四边形EFBD为等腰梯形,EF∥BD,EF=$\frac{1}{2}$BD,平面EFBD⊥平面ABCD.
如图,多面体ABCDEF中,四边形ABCD是边长为2的正方形,四边形EFBD为等腰梯形,EF∥BD,EF=$\frac{1}{2}$BD,平面EFBD⊥平面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
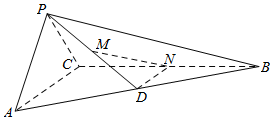 在三棱锥P-ABC中,平面PAC⊥平面ABC,PA⊥PC,AC⊥BC,D为AB的中点,M为PD的中点,N在棱BC上.
在三棱锥P-ABC中,平面PAC⊥平面ABC,PA⊥PC,AC⊥BC,D为AB的中点,M为PD的中点,N在棱BC上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com