
����Ŀ��ij��λ�ٰ�2010���Ϻ�������֪ʶ������������ֳ��齱��
����װ��9�Ŵ�С��ͬ�ľ�����Ƭ����Ƭ�Ϸֱ�ӡ�������������� �����������������Ἢ���ͼ��;�齱�����ǣ��μ��ߴӺ��г�ȡ��Ƭ���ţ����鵽���Ŷ�������������
���ɻ�����Ϊ����.��Ƭ�ú�Żغ��ӣ���һλ�μ������ظ�����.
��1�����ʼ��һλ�μ����ʣ������м��������������������˴���ֻ֪����
�Ӻ��г�ȡ���Ŷ������������������ĸ�����![]() ����齱�ĸ���;
����齱�ĸ���;
��2�����мס��ҡ��������������γ齱����![]() ��ʾ����������
��ʾ����������![]() �ķֲ��м�
�ķֲ��м�![]() ��ֵ.
��ֵ.

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijѧУ��ѧ�ڽ�����Ϊ�˽�ҳ���ѧУ����������ȣ����������100λ�ҳ���������ȵ��飬���������£�
�dz����� | ���� | �ϼ� | |
A | 30 | 15 | 45 |
B | 45 | 10 | 55 |
�ϼ� | 75 | 25 | 100 |
��1�����ݱ����ж��Ƿ���![]() �İ�����Ϊ�ҳ�������̶������ڰ༶�й�ϵ��
�İ�����Ϊ�ҳ�������̶������ڰ༶�й�ϵ��
��2���÷ֲ�����ķ����ӷdz�����ļҳ��г�ȡ5�˽����ʾ����飬������5�������ѡ��2�˽�����̸������2�˶�����ͬһ�༶�ĸ��ʣ�
����
|
|
|
|
|
|
|
|
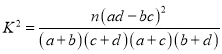
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ʽ|x��1|+|2x+1|��3�Ľ⼯Ϊ{x|a��x��b}��
��1����a��b��ֵ��
��2������ʵ��x��y����x+y��ab+2�Ҳ���ʽ��yc2��4��x+��8cx��1��y��0�������x��y���������ʵ��c��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
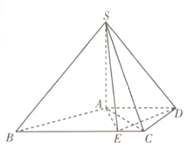
����Ŀ����ͼ��������![]() �У�
�У�![]() ƽ��
ƽ��![]() ������
������![]() ��ֱ�����Σ�
��ֱ�����Σ�![]() ��
��![]() ����
����![]() .��
.��![]() ���߶�
���߶�![]() ��һ�㣬��
��һ�㣬��![]() .
.
��1����֤��ƽ��![]() ƽ��
ƽ��![]() .
.
��2����![]() �����߶�
�����߶�![]() ���Ƿ����һ��
���Ƿ����һ��![]() ��ʹ��
��ʹ��![]() ��ƽ��
��ƽ��![]() �ľ���Ϊ
�ľ���Ϊ![]() �������ڣ���
�������ڣ���![]() ��ֵ���������ڣ���˵������.
��ֵ���������ڣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������![]() ��������ѧ���μ�����һ������������ѧ����ѧ�ɼ������֣�
��������ѧ���μ�����һ������������ѧ����ѧ�ɼ������֣�![]() �֣��Ĵ����ݷ�����֪��������ѧ�ɼ�
�֣��Ĵ����ݷ�����֪��������ѧ�ɼ�![]() ������̬�ֲ�����
������̬�ֲ�����![]() ����
����![]() ��
��![]() .
.
��1����![]() ��ֵ.
��ֵ.
��2���ִӼ��вμӴ˴������ĸ���ѧ���У������ȡ![]() ��ѧ�������ʾ����飬������ѧ�ɼ�����
��ѧ�������ʾ����飬������ѧ�ɼ�����![]() �ֵ�����Ϊ
�ֵ�����Ϊ![]() ����
����![]() .
.
��3����������ڵ�����Ҳ��![]() ��������ѧ���μ��˴˴�������������ѧ�ɼ�
��������ѧ���μ��˴˴�������������ѧ�ɼ�![]() ������̬�ֲ�
������̬�ֲ�![]() .ij��У�涨�˴�������ѧ�ɼ�����
.ij��У�涨�˴�������ѧ�ɼ�����![]() �ֵ�ѧ���ɲμ������������ԣ�������ĸ������ܹ��μ������������Ե�ѧ�����ࣿ
�ֵ�ѧ���ɲμ������������ԣ�������ĸ������ܹ��μ������������Ե�ѧ�����ࣿ
�������������![]() ����
����![]() ��
��![]() ��
��![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����![]() ����
����![]() ������ʵ�����ɵ�һ�����飬������
������ʵ�����ɵ�һ�����飬������![]() .����
.����![]() ������
��Ϊ����![]() �ġ�Ԫ����
�ġ�Ԫ����![]() ��Ϊ
��Ϊ![]() ���±꣬�������
���±꣬�������![]() �е�ÿ����Ԫ��������������
�е�ÿ����Ԫ��������������![]() �в�ͬ�±�ġ�Ԫ�������
�в�ͬ�±�ġ�Ԫ�������![]() Ϊ
Ϊ![]() ��������.������������
��������.������������![]() ��
��![]() �Ĺ�ϵ��Ϊ
�Ĺ�ϵ��Ϊ![]() .
.
��1����![]() ��
��![]() ����
����![]() ��
��![]() �ĺ���������Ԫ���������飬��
�ĺ���������Ԫ���������飬��![]() �����ֵ��
�����ֵ��
��2����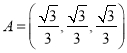 ��
��![]() ����
����![]() ��
��![]() Ϊ
Ϊ![]() �ĺ���������Ԫ���������飬��
�ĺ���������Ԫ���������飬��![]() �����ֵ��
�����ֵ��
��3��������![]() �еġ�Ԫ������
�еġ�Ԫ������![]() ��������
��������![]() �����ĸ���Ԫ��
�����ĸ���Ԫ��![]() ����
����![]() ����
����![]() ��
��![]() �����к���������Ԫ����������Ĺ�ϵ��
�����к���������Ԫ����������Ĺ�ϵ��![]() ��
��![]() �������ֵ.
�������ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x����x3��4x2+5x��4.
��1��������f��x���ڵ㣨2��f��2�����������߷��̣�
��2����g��x����f��x��+k����g��x����������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��.
��.
��1����![]() Ϊ��ֵʱ��ֱ��
Ϊ��ֵʱ��ֱ��![]() ������
������![]() �����ߣ�
�����ߣ�
��2��������ʽ![]() ��
��![]() �Ϻ��������
�Ϻ��������![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������f(x)��xlnx��a��������㣬��ʵ��a��ȡֵ��ΧΪ(����)
A.[0��![]() )B.(0��
)B.(0��![]() )
)
C.(0��![]() ]D.(��
]D.(��![]() ��0)
��0)
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com