
【题目】如图,在四棱锥![]() 中,
中,![]() 平面
平面![]() ,底面
,底面![]() 是直角梯形,
是直角梯形,![]() ,
,![]() ,且
,且![]() .点
.点![]() 是线段
是线段![]() 上一点,且
上一点,且![]() .
.
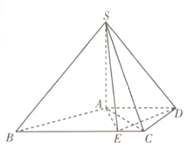
(1)求证:平面![]() 平面
平面![]() .
.
(2)若![]() ,在线段
,在线段![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 到平面
到平面![]() 的距离为
的距离为![]() ?若存在,求
?若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】如图,在正方体ABCD﹣A1B1C1D1中,E,F分别是棱AA1,AD上的点,且AE=EA1,AF![]() FD.
FD.
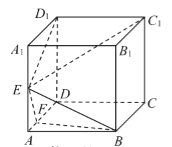
(1)求证:平面EC1D1⊥平面EFB;
(2)求二面角E﹣FB﹣A的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知m,n是两条不同的直线,α,β是两个不同的平面,给出下列命题:
①若m∥n,n⊥β,mα,则α⊥β;
②若α⊥β,α∩β=m,n⊥m,则n⊥α或n⊥β;
③若m⊥α,m⊥n,nβ,则α∥β或α⊥β;
④若α∩β=m,n∥m,nα,nβ,则n∥α且n∥β;
其中正确命题的序号是( )
A.①②B.①③C.①④D.②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,
,
(1)求函数f(x)在x∈[﹣1,2]上的最大值和最小值;
(2)若对于任意x∈[﹣1,2]都有f(x)<m成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() 将圆
将圆![]() 的圆周分为四等份,且椭圆
的圆周分为四等份,且椭圆![]() 的离心率为
的离心率为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() ,且
,且![]() 的中点为
的中点为![]() ,线段
,线段![]() 的垂直平分线为
的垂直平分线为![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位举办2010年上海世博会知识宣传活动,进行现场抽奖,
盒中装有9张大小相同的精美卡片,卡片上分别印有“世博会会徽” 或“海宝”(世博会吉祥物)图案;抽奖规则是:参加者从盒中抽取卡片两张,若抽到两张都是“海宝”卡
即可获奖,否则,均为不获奖.卡片用后放回盒子,下一位参加者继续重复进行.
(1)活动开始后,一位参加者问:盒中有几张“海宝”卡?主持人答:我只知道,
从盒中抽取两张都是“世博会会徽“卡的概率是![]() ,求抽奖者获奖的概率;
,求抽奖者获奖的概率;
(2)现有甲、乙、丙、丁四人依次抽奖,用![]() 表示获奖的人数,求
表示获奖的人数,求![]() 的分布列及
的分布列及![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P-ABC中,![]() ,
,![]() ,
,![]() 平面PAB,D,E分别是AC,BC上的点,且
平面PAB,D,E分别是AC,BC上的点,且![]() 平面PAB.
平面PAB.
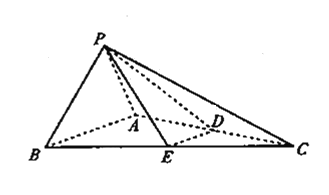
(1)求证![]() 平面PDE;
平面PDE;
(2)若D为线段AC中点,求直线PC与平面PDE所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直四棱柱ABCD-A1B1C1D1中,AD//平面BCC1B1,AD⊥DB.求证:

(1)BC//平面ADD1A1;
(2)平面BCC1B1⊥平面BDD1B1.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com