
【题目】已知 ![]() ,
, ![]() 的夹角为120°,且|
的夹角为120°,且| ![]() |=4,|
|=4,| ![]() |=2.求:
|=2.求:
(1)( ![]() ﹣2
﹣2 ![]() )(
)( ![]() +
+ ![]() );
);
(2)|3 ![]() ﹣4
﹣4 ![]() |.
|.
科目:高中数学 来源: 题型:
【题目】圆x2+y2=8内有一点P0(﹣1,2),AB为过点P0且倾斜角为α的弦;
(1)当 ![]() 时,求AB的长;
时,求AB的长;
(2)当弦AB被点P0平分时,求直线AB的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆C: ![]() +
+ ![]() =1(a>b>0)过点(2,0),离心率为
=1(a>b>0)过点(2,0),离心率为 ![]() .
.
(1)求C的方程;
(2)过点(1,0)且斜率为1的直线l与椭圆C相交于A,B两点,求AB的中点M的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线y2=﹣x与直线y=k(x+1)相交于A(x1 , y1),B(x2 , y2)两点,O为坐标原点.
(1)求y1y2的值;
(2)求证:OA⊥OB.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若关于x的不等式ax2+bx+c<0的解集为({﹣∞,﹣1})∪( ![]() ,+∞),则不等式cx2﹣bx+a<0的解集为( )
,+∞),则不等式cx2﹣bx+a<0的解集为( )
A.(﹣1,2)
B.(﹣∞,﹣1)∪(2,+∞)
C.(﹣2,1)
D.(﹣∞,﹣2)∪(1,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在△ABC中,已知CA=1,CB=2,∠ACB=60°. 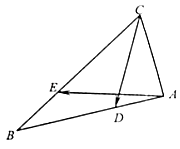
(1)求| ![]() |;
|;
(2)已知点D是AB上一点,满足 ![]() =λ
=λ ![]() ,点E是边CB上一点,满足
,点E是边CB上一点,满足 ![]() =λ
=λ ![]() . ①当λ=
. ①当λ= ![]() 时,求
时,求 ![]()
![]() ;
;
②是否存在非零实数λ,使得 ![]() ⊥
⊥ ![]() ?若存在,求出的λ值;若不存在,请说明理由.
?若存在,求出的λ值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知{an}是各项均为正数的等比数列a1+a2=2( ![]() ),a3+a4+a5=64
),a3+a4+a5=64 ![]() +
+ ![]() +
+ ![]() )
)
(1)求{an}的通项公式;
(2)设bn=(an+ ![]() )2 , 求数列{bn}的前n项和Tn .
)2 , 求数列{bn}的前n项和Tn .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com