
【题目】已知![]() 为等差数列,前n项和为
为等差数列,前n项和为![]() ,
, ![]() 是首项为2的等比数列,且公比大于0,
是首项为2的等比数列,且公比大于0, ![]() ,
,![]() ,
, ![]() .
.
(Ⅰ)求![]() 和
和![]() 的通项公式;
的通项公式;
(Ⅱ)求数列![]() 的前n项和
的前n项和![]() .
.
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:高中数学 来源: 题型:
【题目】已知向量 ![]() ,函数f(x)=
,函数f(x)= ![]()
![]() +2.
+2.
(1)求函数f(x)的最小正周期;
(2)设锐角△ABC内角A,B,C所对的边分别为a,b,c,若f(A)=2, ![]() ,求角A和边c的值.
,求角A和边c的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知长方体AC1中,AD=AB=2,AA1=1,E为D1C1的中点,如图所示.
(Ⅰ)在所给图中画出平面ABD1与平面B1EC的交线(不必说明理由);
(Ⅱ)证明:BD1∥平面B1EC;
(Ⅲ)求平面ABD1与平面B1EC所成锐二面角的大小.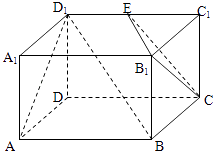
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=|2x﹣1|,定义f1(x)=x,fn+1(x)=f(fn(x)),已知函数g(x)=fm(x)﹣x有8个零点,则m的值为( )
A.8
B.4
C.3
D.2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() ,已知定义在R上的函数
,已知定义在R上的函数![]() 在区间
在区间![]() 内有一个零点
内有一个零点![]() ,
, ![]() 为
为![]() 的导函数.
的导函数.
(Ⅰ)求![]() 的单调区间;
的单调区间;
(Ⅱ)设![]() ,函数
,函数![]() ,求证:
,求证: ![]() ;
;
(Ⅲ)求证:存在大于0的常数![]() ,使得对于任意的正整数
,使得对于任意的正整数![]() ,且
,且![]() 满足
满足![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足:a1=1,an+1= ![]() an+
an+ ![]()
![]() (n∈N*).
(n∈N*).
(1)求最小的正实数M,使得对任意的n∈N* , 恒有0<an≤M.
(2)求证:对任意的n∈N* , 恒有 ![]() ≤an≤
≤an≤ ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2﹣2lnx,h(x)=x2﹣x+a.
(1)其求函数f(x)的极值;
(2)设函数k(x)=f(x)﹣h(x),若函数k(x)在[1,3]上恰有两个不同零点求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着我市九龙江南岸江滨路建设的持续推进,未来市民将新增又一休闲好去处,据悉南江滨路建设工程规划配套建造一个长方形公园ABCD,如图所示,公园由长方形的休闲区A1B1C1D1(阴影部分)和环公园人行道组成,已知休闲区A1B1C1D1的面积为4000m2 , 人行道的宽度分别为4m和10m.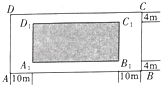
(1)若休闲区的长A1B1=x m,求公园ABCD所占面积S关于x的函数S(x)的解析式;
(2)要使公园所占面积最小,休闲区A1B1C1D1的长和宽该如何设计?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com