
【题目】已知数列{an}满足:a1=1,an+1= ![]() an+
an+ ![]()
![]() (n∈N*).
(n∈N*).
(1)求最小的正实数M,使得对任意的n∈N* , 恒有0<an≤M.
(2)求证:对任意的n∈N* , 恒有 ![]() ≤an≤
≤an≤ ![]() .
.
【答案】
(1)解:最小的正实数M=1,即使得对任意的n∈N*,恒有0<an≤1.
下面利用数学归纳法证明:①当n=1时,a1=1成立;
②假设n=k(k∈N*)时,对任意的k∈N*,恒有0<ak≤1.
则n=k+1时,易知k<2k,
∴0<ak+1= ![]() +
+ ![]()
![]() <
< ![]() ≤
≤ ![]() <
< ![]() +
+ ![]() =1,
=1,
因此当n=k+1时假设成立,
综上可得:最小的正实数M=1,使得对任意的n∈N*,恒有0<an≤M
(2)证明:先证明右边:由(1)可得:0<an≤1.
∴an+1= ![]() an+
an+ ![]() =an
=an ![]() ≤an(
≤an( ![]() )≤an(
)≤an( ![]() )≤an(
)≤an( ![]() )=
)= ![]() an,(2n≤2n).
an,(2n≤2n).
∴an≤ ![]() ≤
≤ ![]() =
= ![]() ,因此右边成立.
,因此右边成立.
证明左边:下面利用数学归纳法证明:①当n=1时,a1=1= ![]() ,成立;
,成立;
②假设n=k(k∈N*)时,对任意的k∈N*,恒有ak≥ ![]() .
.
则n=k+1时,要证明:ak+1≥ ![]() ,
,
又ak+1= ![]() +
+ ![]()
![]() ,
,
∴只要证明: ![]() +
+ ![]()
![]() ≥
≥ ![]() ,
,
化为:k(5×2k+4) ![]() +2kak﹣182k≥0,
+2kak﹣182k≥0,
解出:ak≥ ![]() ≥
≥ ![]() =
= ![]() .
.
因此当n=k+1时也成立,
综上①②可得:左边成立.
因此:对任意的n∈N*,恒有 ![]() ≤an≤
≤an≤ ![]()
【解析】(1)最小的正实数M=1,即使得对任意的n∈N* , 恒有0<an≤1.利用数学归纳法即可证明.(2)先证明右边:由(1)可得:0<an≤1.通过放缩:an+1= ![]() an+
an+ ![]()
![]() =an
=an ![]() ≤an(
≤an( ![]() )
) ![]() an , (2n≤2n).可得:an≤
an , (2n≤2n).可得:an≤ ![]() .证明左边:利用数学归纳法证明即可得出.
.证明左边:利用数学归纳法证明即可得出.
【考点精析】掌握数列的前n项和和数列的通项公式是解答本题的根本,需要知道数列{an}的前n项和sn与通项an的关系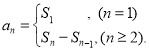 ;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.
;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.


科目:高中数学 来源: 题型:
【题目】如图,在棱长为a的正方体ABCD﹣A1B1C1D1中,P为A1D1的中点,Q为A1B1上任意一点,E,F为CD上任意两点,且EF的长为定值b,则下面的四个值中不为定值的是( ) 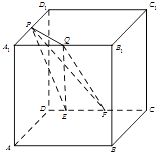
A.点P到平面QEF的距离
B.三棱锥P﹣QEF的体积
C.直线PQ与平面PEF所成的角
D.二面角P﹣EF﹣Q的大小
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于给定的正整数k,若数列{an}满足![]()
=2kan对任意正整数n(n> k) 总成立,则称数列{an} 是“P(k)数列”.
(1)证明:等差数列{an}是“P(3)数列”;
若数列{an}既是“P(2)数列”,又是“P(3)数列”,证明:{an}是等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从甲地到乙地要经过3个十字路口,设各路口信号灯工作相互独立,且在各路口遇到红灯的概率分别为![]() .
.
(Ⅰ)设![]() 表示一辆车从甲地到乙地遇到红灯的个数,求随机变量
表示一辆车从甲地到乙地遇到红灯的个数,求随机变量![]() 的分布列和数学期望;
的分布列和数学期望;
(Ⅱ)若有2辆车独立地从甲地到乙地,求这2辆车共遇到1个红灯的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在长方体ABCD﹣A1B1C1D1中,AB=5,AD=8,AA1=4,M为B1C1上一点且B1M=2,点N在线段A1D上,A1D⊥AN. 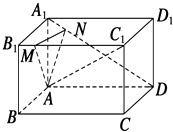
(1)求直线A1D与AM所成角的余弦值;
(2)求直线AD与平面ANM所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
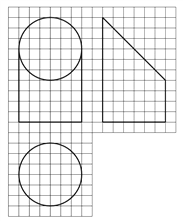
【题目】如图,网格纸上小正方形的边长为![]() ,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分所得,则该几何体的体积为( )
,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分所得,则该几何体的体积为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com