
分析 (1)分类讨论,求导数,切点函数的单调性,即可讨论h(x)零点的个数;
(2)设出切点,由切线方程,化简得三次函数,将题目条件化为函数有三个零点,即可求a的取值范围.
解答 解:(1)f′(x)=(2x+1)(x-1)2=0,x=-$\frac{1}{2}$或1,∴x=-$\frac{1}{2}$是h(x)的零点;
∵g′(x)=k-$\frac{1}{x}$,
k<0,g′(x)<0,g(x)在[1,+∞)上单调递减,g(x)的最大值为g(1)=k+1.
k<-1,g(1)<0,g(x)在[1,+∞)上无零点;
k=-1,g(1)=0,g(x)在[1,+∞)上有1个零点;
-1<k<0,g(1)>0,g(e1-k)=ke1-k+k<0,g(x)在[1,+∞)上有1个零点;
综上所述,k<-1时,h(x)有1个零点;-1≤k<0时,h(x)有两个零点;
(2)设切点(t,f(t)),f′(x)=6x2-6x,∴切线斜率f′(t)=6t2-6t,
∴切线方程为y-f(t)=(6t2-6t)(x-t),
∵切线过P(a,-4),∴-4-f(t)=(6t2-6t)(a-t),
∴4t3-3t2-6t2a+6ta-5=0①
由题意,方程①有3个不同的解.
令H(t)=4t3-3t2-6t2a+6ta-5,则H′(t)=12t2-6t-12at+6a=0.t=$\frac{1}{2}$或a.
a=$\frac{1}{2}$时,H′(t)≥0,H(t)在定义域内单调递增,H(t)不可能有两个零点,方程①不可能有两个解,不满足题意;
a$>\frac{1}{2}$时,在(-$∞,\frac{1}{2}$),(a,+∞)上,H′(t)>0,函数单调递增,在($\frac{1}{2}$,a)上,H′(t)<0,函数单调递减,H(t)的极大值为H($\frac{1}{2}$),极小值为H(a);
a$<\frac{1}{2}$时,在(-∞,a),($\frac{1}{2}$,+∞)上,H′(t)>0,函数单调递增,在(a,$\frac{1}{2}$)上,H′(t)<0,函数单调递减,H(t)的极大值为H(a),极小值为H($\frac{1}{2}$);
要使方程①有三个不同解,则H($\frac{1}{2}$)H(a)<0,即(2a-7)(a+1)(2a2-5a+5)>0,
∴a>$\frac{7}{2}$或a<-1.
点评 本题考查了导数的综合应用,同时考查了斜率的表示方法,用到函数零点个数的判断,属于难题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{16}$ | B. | $\frac{3}{8}$ | C. | $\frac{5}{8}$ | D. | $\frac{11}{16}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,+∞) | B. | (-∞,0) | C. | (-1,+∞) | D. | (-∞,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-$\frac{1}{4}$,$\frac{1}{4}$) | B. | [-$\frac{1}{4}$,$\frac{1}{4}$] | C. | (-∞,-$\frac{1}{4}$]∪(0,$\frac{1}{4}$) | D. | (-∞,-$\frac{1}{4}$]∪[$\frac{1}{4}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
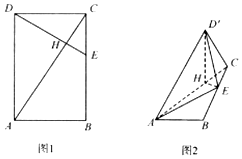 如图1,已知矩形ABCD中,$AB=2,BC=2\sqrt{3}$,点E是边BC上的点,且$CE=\frac{1}{3}CB$,DE与AC相交于点H.现将△ACD沿AC折起,如图2,点D的位置记为D',此时$D'E=\frac{{\sqrt{30}}}{3}$.
如图1,已知矩形ABCD中,$AB=2,BC=2\sqrt{3}$,点E是边BC上的点,且$CE=\frac{1}{3}CB$,DE与AC相交于点H.现将△ACD沿AC折起,如图2,点D的位置记为D',此时$D'E=\frac{{\sqrt{30}}}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
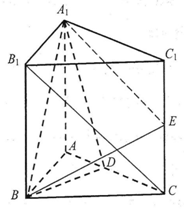 如图,侧棱垂直于底面的三棱柱ABC-A1B1C1中,D,E分别是AC,CC1的中点,$AB=BC=A{A_1}=\frac{{\sqrt{2}}}{2}AC$.
如图,侧棱垂直于底面的三棱柱ABC-A1B1C1中,D,E分别是AC,CC1的中点,$AB=BC=A{A_1}=\frac{{\sqrt{2}}}{2}AC$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com