
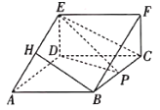
【题目】如图,在三棱柱![]() 中,
中,![]() 是边长为2的菱形,且
是边长为2的菱形,且![]() ,
,![]() 是矩形,
是矩形,![]() ,且平面
,且平面![]() 平面
平面![]() ,
,![]() 点在线段
点在线段![]() 上移动(
上移动(![]() 不与
不与![]() 重合),
重合),![]() 是
是![]() 的中点.
的中点.
(1)当四面体![]() 的外接球的表面积为
的外接球的表面积为![]() 时,证明:
时,证明:![]() .平面
.平面![]()
(2)当四面体![]() 的体积最大时,求平面
的体积最大时,求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
【答案】(1)证明见解析(2)![]()
【解析】
(1)由题意,先求得![]() 为
为![]() 的中点,再证明平面
的中点,再证明平面![]() 平面
平面![]() ,进而可得结论;
,进而可得结论;
(2)由题意,当点![]() 位于点
位于点![]() 时,四面体
时,四面体![]() 的体积最大,再建立空间直角坐标系,利用空间向量运算即可.
的体积最大,再建立空间直角坐标系,利用空间向量运算即可.
(1)证明:当四面体![]() 的外接球的表面积为
的外接球的表面积为![]() 时.
时.
则其外接球的半径为![]() .
.
因为![]() 时边长为2的菱形,
时边长为2的菱形,![]() 是矩形.
是矩形.
![]() ,且平面
,且平面![]() 平面
平面![]() .
.
则![]() ,
,![]() .
.
则![]() 为四面体
为四面体![]() 外接球的直径.
外接球的直径.
所以![]() ,即
,即![]() .
.
由题意,![]() ,
,![]() ,所以
,所以![]() .
.
因为![]() ,所以
,所以![]() 为
为![]() 的中点.
的中点.
记![]() 的中点为
的中点为![]() ,连接
,连接![]() ,
,![]() .
.

则![]() ,
,![]() ,
,![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
因为![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
(2)由题意,![]() 平面
平面![]() ,则三棱锥
,则三棱锥![]() 的高不变.
的高不变.
当四面体![]() 的体积最大时,
的体积最大时,![]() 的面积最大.
的面积最大.
所以当点![]() 位于点
位于点![]() 时,四面体
时,四面体![]() 的体积最大.
的体积最大.
以点![]() 为坐标原点,建立如图所示的空间直角坐标系
为坐标原点,建立如图所示的空间直角坐标系![]() .
.
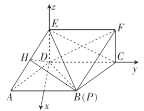
则![]() ,
,![]() ,
,![]() ,
,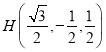 ,
,![]() .
.
所以![]() ,
,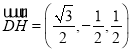 ,
,![]() ,
,![]() .
.
设平面![]() 的法向量为
的法向量为![]() .
.
则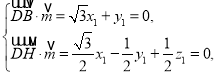
令![]() ,得
,得![]() .
.
设平面![]() 的一个法向量为
的一个法向量为![]() .
.
则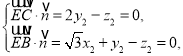
令![]() ,得
,得![]() .
.
设平面![]() 与平面
与平面![]() 所成锐二面角是
所成锐二面角是![]() ,则
,则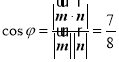 .
.
所以当四面体![]() 的体积最大时,平面
的体积最大时,平面![]() 与平面
与平面![]() 所成锐二面角的余弦值为
所成锐二面角的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】“伟大的变革—庆祝改革开放40周年大型展览”于2019年3月20日在中国国家博物馆闭幕,本次特展紧扣“改革开放40年光辉历程”的主线,多角度、全景式描绘了我国改革开放40年波澜壮阔的历史画卷.据统计,展览全程呈现出持续火爆的状态,现场观众累计达423万人次,参展人数屡次创造国家博物馆参观纪录,网上展馆点击浏览总量达4.03亿次.
下表是2019年2月参观人数(单位:万人)统计表
日期 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
人数 | 3.0 | 3.1 | 2.5 | 2.3 | 5.4 | 6.8 | 6.2 | 6.7 | 5.5 | 4.9 | 3.2 | 3.0 | 2.7 | 2.5 |
日期 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 |
人数 | 2.4 | 2.9 | 3.2 | 2.8 | 2.9 | 2.3 | 3.0 | 2.9 | 3.1 | 3.0 | 3.1 | 3.1 | 3.1 | 3.0 |
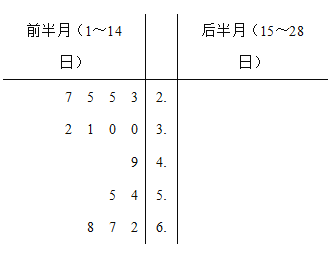
根据表中数据回答下列问题:
(1)请将2019年2月前半月(1~14日)和后半月(15~28日)参观人数统计对比茎叶图填补完整,并通过茎叶图比较两组数据方差的大小(不要求计算出具体值,得出结论即可);
(2)将2019年2月参观人数数据用该天的对应日期作为样本编号,现从中抽样7天的样本数据.若抽取的样本编号是以4为公差的等差数列,且数列的第4项为15,求抽出的这7个样本数据的平均值;
(3)根据国博以往展览数据及调查统计信息可知,单日入馆参观人数为0~3(含3,单位:万人)时,参观者的体验满意度最佳,在从(2)中抽出的样本数据中随机抽取两天的数据,求这两天参观者的体验满意度均为最住的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() 的最大值为
的最大值为![]() .
.
(Ⅰ)求实数![]() 的值;
的值;
(Ⅱ)当![]() 时,讨论函数
时,讨论函数![]() 的单调性;
的单调性;
(Ⅲ)当![]() 时,令
时,令![]() ,是否存在区间
,是否存在区间![]() .使得函数
.使得函数![]() 在区间
在区间![]() 上的值域为
上的值域为![]() 若存在,求实数
若存在,求实数![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知曲线
中,已知曲线![]() 的参数方程为
的参数方程为![]() (
(![]() ,
, ![]() 为参数).以坐标原点
为参数).以坐标原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴,取相同的长度单位建立极坐标系,直线
轴的正半轴为极轴,取相同的长度单位建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)当![]() 时,求曲线
时,求曲线![]() 上的点到直线
上的点到直线![]() 的距离的最大值;
的距离的最大值;
(2)若曲线![]() 上的所有点都在直线
上的所有点都在直线![]() 的下方,求实数
的下方,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,已知四边形
中,已知四边形![]() 是边长为
是边长为![]() 的正方形,点
的正方形,点![]() 是
是![]() 的中点,点
的中点,点![]() 在底面
在底面![]() 上的射影为点
上的射影为点![]() ,点
,点![]() 在棱
在棱![]() 上,且四棱锥
上,且四棱锥![]() 的体积为
的体积为![]() .
.
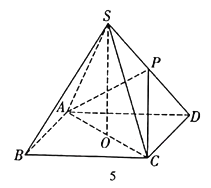
(1)若点![]() 是
是![]() 的中点,求证:平面
的中点,求证:平面![]() 平面
平面![]() ;
;
(2)若二面角![]() 的余弦值为
的余弦值为![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在矩形![]() 中,已知
中,已知![]() ,
,![]() ,点
,点![]() ,
,![]() 分别在边
分别在边![]() ,
,![]() 上,且
上,且![]() ,将梯形
,将梯形![]() 沿
沿![]() 折起,使
折起,使![]() 在平面
在平面![]() 上的射影
上的射影![]() 恰好落在线段
恰好落在线段![]() 靠近
靠近![]() 的三等分点处,得到图2中的立体图形.
的三等分点处,得到图2中的立体图形.
(1)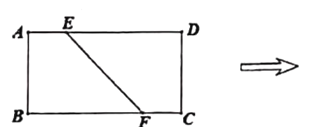 (2)
(2) 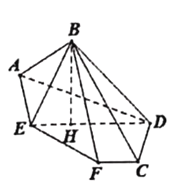
(1)在图2中,求证:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国家每年都会对中小学生进行体质健康监测,一分钟跳绳是监测的项目之一.今年某小学对本校六年级300名学生的一分钟跳绳情况做了统计,发现一分钟跳绳个数最低为10,最高为189.现将跳绳个数分成![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 6组,并绘制出如下的频率分布直方图.
6组,并绘制出如下的频率分布直方图.
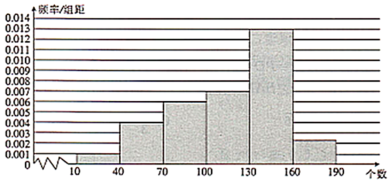
(1)若一分钟跳绳个数达到160为优秀,求该校六年级学生一分钟跳绳为优秀的人数;
(2)上级部门要对该校体质监测情况进行复查,发现每组男、女学生人数比例有很大差别,![]() 组男、女人数之比为
组男、女人数之比为![]() ,
,![]() 组男、女人数之比为
组男、女人数之比为![]() ,
,![]() 组男、女人数之比为
组男、女人数之比为![]() ,
,![]() 组男、女人数之比为
组男、女人数之比为![]() ,
,![]() 组男、女人数之比为
组男、女人数之比为![]() ,
,![]() 组男、女人数之比为
组男、女人数之比为![]() .试估计此校六年级男生一分钟跳绳个数的平均数(同一组中的数据用该组区间的中点值作代表,结果保留整数).
.试估计此校六年级男生一分钟跳绳个数的平均数(同一组中的数据用该组区间的中点值作代表,结果保留整数).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于函数![]() ,下列说法正确的是( )
,下列说法正确的是( )
(1)![]() 是
是![]() 的极小值点;
的极小值点;
(2)函数![]() 有且只有1个零点;
有且只有1个零点;
(3)![]() 恒成立;
恒成立;
(4)设函数![]() ,若存在区间
,若存在区间![]() ,使
,使![]() 在
在![]() 上的值域是
上的值域是![]() ,则
,则![]() .
.
A.(1) (2)B.(2)(4)C.(1) (2) (4)D.(1)(2)(3)(4)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com