
| 使用年限x | 1 | 2 | 3 | 4 | 5 |
| 维修费用y | 5 | 6 | 7 | 8 | 10 |
分析 (1)利用描点法可得图象;
(2)根据所给的数据,做出变量x,y的平均数,求出b,a的值;
(3)当自变量为10时,代入线性回归方程,求出维修费用,这是一个预报值.
解答 解:(1)散点图如下: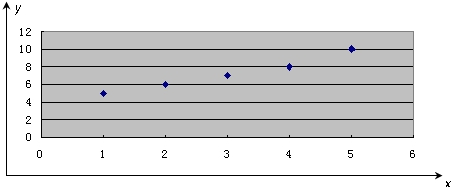
…(4分)
(2)列表计算如下
| i | xi | yi | xi2 | xiyi |
| 1 | 1 | 5 | 1 | 5 |
| 2 | 2 | 6 | 4 | 12 |
| 3 | 3 | 7 | 9 | 21 |
| 4 | 4 | 8 | 16 | 32 |
| 5 | 5 | 10 | 25 | 50 |
| 15 | 36 | 55 | 120 |
点评 本题考查线性回归方程的求解和应用,是一个基础题,解题的关键是正确应用最小二乘法来求线性回归方程的系数.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $2\sqrt{7}$ | B. | $\sqrt{60}$ | C. | $7\sqrt{2}$ | D. | $\sqrt{30}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | k+1 | B. | 2k+1 | C. | k2+1 | D. | (k+1)2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com