
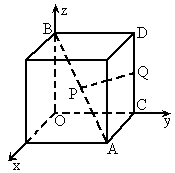
如图,以正方体的三条棱所在直线为坐标轴,建立空间直角坐标系O-xyz,点P在对角线AB上运动,点Q为棱CD的中点,探求|PQ|的最小值.
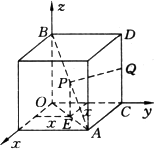
科目:高中数学 来源: 题型:044
如图
,以正方体的三条棱所在直线为坐标轴,建立空间直角坐标系O-xyz,点P在正方体的对角线AB上,点Q在正方体的棱CD上.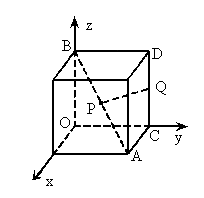
(1)
当点P为对角线AB的中点,点Q在棱CD上运动时,探究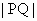 的最小值;
的最小值;
(2)
当点Q为棱CD的中点,点P在对角线AB上运动时,探究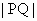 的最小值;
的最小值;
(3)
当点P在对角线AB上运动,点Q在棱CD上运动时,探究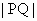 的最小值.
的最小值.
由以上问题,你得到了什么结论,你能证明你的结论吗?
查看答案和解析>>
科目:高中数学 来源:数学教研室 题型:044
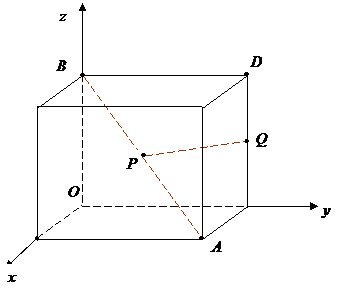
如图,以正方体的三条棱所在直线为坐标轴,建立空间直角坐标系O-xyz,点P在正方体的对角线AB上,点Q在正方体的棱CD上.
(1)当点P为对角线AB的中点,点在Q在棱CD上运动时,探究|PQ|的最小值;
(2)当点Q为棱CD的中点,点P在对角线上运动时,探究|PQ|的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,以正方体的三条棱所在直线为坐标轴,建立空间直角坐标系![]() .点
.点![]() 在正方体的对角线
在正方体的对角线![]() 上,点
上,点![]() 在正方体的棱
在正方体的棱![]() 上.
上.
当点![]() 为对角线
为对角线![]() 的中点,点
的中点,点![]() 在棱
在棱![]() 上运动时,探究
上运动时,探究![]() 的最小值;
的最小值;
当点![]() 为棱
为棱![]() 的中点,点
的中点,点![]() 在对角线
在对角线![]() 上运动时,探究
上运动时,探究![]() 的最小值;
的最小值;
当点![]() 在对角线
在对角线![]() 上运动,点
上运动,点![]() 在棱
在棱![]() 上运动时,探究
上运动时,探究![]() 的最小值.
的最小值.
由以上问题,你得到了什么结论?你能证明你的结论吗?
查看答案和解析>>
科目:高中数学 来源:2010年湖北省高二期中考试文科数学试卷 题型:解答题
(本小题满分12分)如图在棱长为1正方体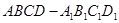 中,以正方体的三条棱所在直线为轴建立空间直角坐标系
中,以正方体的三条棱所在直线为轴建立空间直角坐标系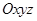 ,
,
(I)若点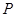 在线段
在线段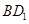 上,且满足
上,且满足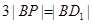 ,试写出点
,试写出点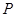 的坐标并写出
的坐标并写出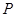 关于平面
关于平面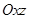 的对称点
的对称点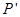 的坐标;
的坐标;
(Ⅱ)线段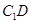 中点为
中点为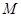 ,求点
,求点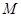 到点
到点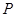 的距离。
的距离。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com