练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    5．在等差数列{an}中，a1=2，a7=20，求S15．

    分析 根据题意，设等差数列{an}的公差为d，又由a1、a7的值，结合等差数列通项公式可得d的值，进而可得a15的值，由等差数列前n项和公式S15=$\frac{（{a}_{1}+{a}_{15}）×15}{2}$，代入数据计算可得答案．

    解答 解：根据题意，设等差数列{an}的公差为d，
    又由a1=2，a7=20，则a7=a1+6d=2+6d=20，
    解可得d=3，
    则a15=a1+14d=44，
    故S15=$\frac{（{a}_{1}+{a}_{15}）×15}{2}$=$\frac{（2+44）×15}{2}$=345；
    故S15=345．

    点评 本题考查等差数列前n项和的计算，注意要根据题意，求出等差数列的通项公式．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    15．已知函数f（x）=x2-3x+m+1nx（m∈R）
    （1）求f（x）的单调增区间与减区间；
    （2）填表（不要求过程，只填结果即可）
    m的范围   
    方程f（x）=0的解得个数123

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

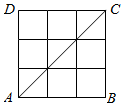    16．如图，ABCD为边长为3的正方形，把各边三等分后，共有16个交点，从中选取两个交点作为向量，则与$\overrightarrow{AC}$平行且长度为2$\sqrt{2}$的向量个数有8个．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    13．递增等比数列{an}中，已知a1+a4=9，a2a3=8，则通项an=2n-1．设bn=2log2an+3，则数列{$\frac{1}{{{b}_{n}b}_{n+2}}$}前n项和Sn=$\frac{2}{15}$-$\frac{n+2}{（2n+3）（2n+5）}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    20．已知sin2α=$\frac{5}{13}$，α∈（$\frac{π}{4}$，$\frac{π}{2}$），求sin4α，cos4α，tan4α的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    10．与α终边关于x轴对称的角的集合为{β|β=-α+2kπ，k∈Z}．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    17．向量$\overrightarrow{a}$，$\overrightarrow{b}$满足|$\overrightarrow{a}$|=6，|$\overrightarrow{b}$|=10，则|$\overrightarrow{a}$+$\overrightarrow{b}$|的最大值是16，最小值是4．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    14．在三角形△ABC中，bsinA=$\sqrt{3}$acosB，则B=$\frac{π}{3}$；若b=2$\sqrt{2}$，则△ABC面积最大值为2$\sqrt{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    15．函数f（x）=sin2x+2acosx-a-3．
    （I）当a=2时，求f（x）最大值．
    （Ⅱ）若f（x）的最大值为2，求a的值．

    查看答案和解析>>

    同步练习册答案