练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    16．已知函数f（x）=（x-2）ex，其中e是自然对数的底数．
    （1）求函数f（x）的单调区间；
    （2）当x∈[0，4]时，求函数f（x）的最小值．

    分析 （1）求出函数的导数，解关于导函数的不等式，求出函数的单调区间即可；
    （2）根据函数的单调性，求出函数在闭区间的最小值即可．

    解答 解：（1）因为f（x）=（x-2）ex，所以f'（x）=（x-1）ex．
    令f'（x）=0，得x=1．
    当x＜1时，f'（x）＜0；当x＞1时，f'（x）＞0；
    所以函数f（x）=（x-2）ex的单调递减区间是（-∞，1），单调递增区间是（1，+∞）．
    （2）当x变化时，f'（x）与f（x）的变化关系如下表：

    x0（0，1）1（1，4）4
    f'（x）-+
    f（x）-2↓-e↑2 e4
    所以当x=1时，函数f（x）有最小值-e．

    点评 本题考查了函数的单调性、最值问题，考查导数的应用，是一道中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    6．已知$α∈（\frac{π}{2}，π）$，且$sinα=\frac{4}{5}$．
    （1）求$cos（α-\frac{π}{4}）$的值；
    （2）求${sin^2}\frac{α}{2}+\frac{sin4αcos2α}{1+cos4α}$的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．已知数列{an}的前n项和为Sn，且满足a1=1，2Sn=（n+1）an，数列{bn}中，bn=2${\;}^{{a}_{n}+1}$．
    （Ⅰ）求数列{an}，{bn}的通项公式；
    （Ⅱ）求数列{$\frac{1}{{a}_{n}•（lo{g}_{2}{b}_{n}）}$}的前n项和Tn．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

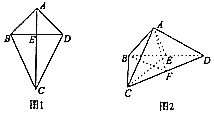    4．如图1，四边形ABCD中AC⊥BD，CE=2AE=2BE=2DE=2，将四边形ABCD沿着BD折叠，得到图2所示的三棱锥A-BCD，其中AB⊥CD．
    （Ⅰ）证明：平面ACD⊥平面BAD；
    （Ⅱ）若F为CD中点，求二面角C-AB-F的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    11．设函数f（x）=ln（x+1）+a（x2-x），其中a∈R
    （1）讨论函数f（x）极值点的个数，并说明理由；
    （2）若任意x∈（0，+∞），f（x）＞0成立，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    1．已知在四棱柱ABCD-A1B1C1D1，侧棱AA1⊥底面ABCD，AB⊥AD，BC∥AD，且AB=2，AD=4，BC=1，侧棱AA1=4．
    （1）若E为AA1上一点，试确定E点的位置，使EB∥平面A1CD；
    （2）在（1）的条件下，求二面角E-BD-A的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．设△ABC的三内角A、B、C的对边分别是a、b、c，且b（sinB-sinC）+（c-a）（sinA+sinC）=0
    （Ⅰ）求角A的大小；
    （Ⅱ）若a=$\sqrt{3}$，sinC=$\frac{{1+\sqrt{3}}}{2}$sinB，求△ABC的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．在平面直角坐标系，将曲线C1上的每一个点的横坐标保持不变，纵坐标缩短为原来的$\frac{1}{2}$，得到曲线C2，以坐标原点O为极点，x轴的正半轴为极轴，建立极坐标系，曲线C1的极坐标方程为ρ=2．
    （Ⅰ）求曲线C2的参数方程；
    （Ⅱ）过原点O且关于y轴对称点两条直线l1与l2分别交曲线C2于A、C和B、D，且点A在第一象限，当四边形ABCD的周长最大时，求直线l1的普通方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．已知函数f（x）=ex（lnx+x-1）．
    （1）求函数f（x）在点（1，f（1））处的切线方程；
    （2）试比较f（x）与1的大小．

    查看答案和解析>>

    同步练习册答案