思路分析:在一定条件下,“利润最大”“用料最省”“面积最大”“效率最高”“强度最大”等问题,在生产、生活中经常用到,在数学上这类问题往往归结为求函数的最值问题.除了常见的求最值的方法外,还可用求导法求函数的最值.但无论采取何种方法都必须在函数的定义域内进行.
解法一:设相同的时间内,生产第x(x∈N*,1≤x≤10)档次的产品利润y最大. 2分
依题意,得y=[8+2(x-1)][60-3(x-1)] 4分
=-6x2+108x+378=-6(x-9)2+864(1≤x≤10), 8分
显然,当x=9时,ymax=864(元),
即在相同的时间内,生产第9档次的产品的总利润最大,最大利润为864元. 10分
解法二:由上面解法得到y=-6x2+108x+378.
求导数,得y′=-12x+108,令y′=-12x+108=0,
解得x=9.因x=9∈[1,10],y只有一个极值点,所以它是最值点,即在相同的时间内,生产第9档次的产品利润最大,最大利润为864元.
【名师指引】一般情况下,对于实际生活中的优化问题,如果其目标函数为高次多项式函数、简单的分式函数简单的无理函数、简单的指数、对数函数,或它们的复合函数,均可用导数法求其最值.由此也可见,导数的引入,大大拓宽了中学数学知识在实际优化问题中的应用空间.



 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案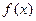 ,
,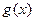 是定义在R上的函数,
是定义在R上的函数,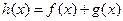 ,则“
,则“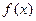 ,
,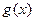 均为偶函数”是“
均为偶函数”是“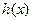 为偶函数”的
为偶函数”的