
设数列{an}的前n项和为Sn.已知a1=1,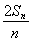 =an+1-
=an+1-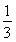 n2-n-
n2-n-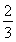 ,n∈N*.
,n∈N*.
(1)求a2的值;
(2)求数列{an}的通项公式;
(3)证明:对一切正整数n,有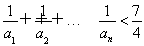 .
.
(1)a2=4.(2)an=n2,n∈N*(3)见解析
【解析】(1)【解析】
∵ =an+1-
=an+1-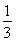 n2-n-
n2-n-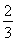 ,n∈N?.
,n∈N?.
∴当n=1时,2a1=2S1=a2-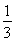 -1-
-1-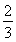 =a2-2.
=a2-2.
又a1=1,∴a2=4.
(2)【解析】
∵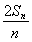 =an+1-
=an+1-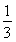 n2-n-
n2-n-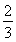 ,n∈N?.
,n∈N?.
∴2Sn=nan+1-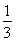 n3-n2-
n3-n2-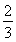 n=nan+1-
n=nan+1-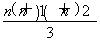 ,①
,①
∴当n≥2时,2Sn-1=(n-1)an-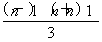 ,②
,②
由①-②,得2Sn-2Sn-1=nan+1-(n-1)an-n(n+1),
∵2an=2Sn-2Sn-1,∴2an=nan+1-(n-1)an-n(n+1),∴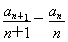 =1,
=1,
∴数列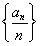 是以首项为
是以首项为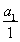 =1,公差为1的等差数列.
=1,公差为1的等差数列.
∴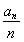 =1+1×(n-1)=n,∴an=n2(n≥2),
=1+1×(n-1)=n,∴an=n2(n≥2),
当n=1时,上式显然成立. ∴an=n2,n∈N*.
(3)证明:由(2)知,an=n2,n∈N*,
①当n=1时,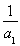 =1<
=1<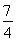 ,∴原不等式成立.
,∴原不等式成立.
②当n=2时,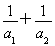 =1+
=1+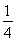 <
<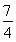 ,∴原不等式成立.
,∴原不等式成立.
③当n≥3时,∵n2>(n-1)·(n+1),
∴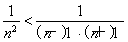 , ∴
, ∴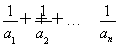 =
=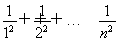
<1+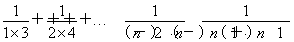
=1+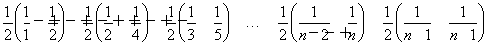
=1+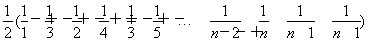
=1+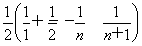 =
=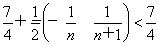 ,
,
∴当n≥3时,∴原不等式亦成立.
综上,对一切正整数n,有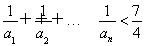 .
.


科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第八章第4课时练习卷(解析版) 题型:解答题
如图,在三棱锥SABC中,平面SAB⊥平面SBC,AB⊥BC,AS=AB,过A作AF⊥SB,垂足为F,点E、G分别是棱SA、
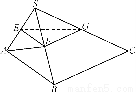
SC的中点.求证:
(1)平面EFG∥平面ABC;
(2)BC⊥SA.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第八章第2课时练习卷(解析版) 题型:填空题
在梯形ABCD中,AB∥CD,AB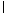 平面α,CD
平面α,CD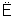 平面α,则直线CD与平面α内的直线的位置关系可能是________.
平面α,则直线CD与平面α内的直线的位置关系可能是________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第八章第1课时练习卷(解析版) 题型:填空题
已知点P、Q,平面α,将命题“P∈α,Q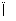 α
α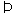 PQ
PQ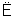 α”改成文字叙述是________.
α”改成文字叙述是________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第五章第6课时练习卷(解析版) 题型:填空题
若等差数列的前6项和为23,前9项和为57,则数列的前n项和Sn=________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第五章第6课时练习卷(解析版) 题型:填空题
已知等差数列{an}的前n项和为Sn,若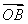 =a100·
=a100·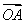 +a101
+a101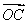 ,且A、B、C三点共线(该直线不过点O),则S200=________.
,且A、B、C三点共线(该直线不过点O),则S200=________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第五章第5课时练习卷(解析版) 题型:解答题
设{an}是公比不为1的等比数列,其前n项和为Sn,且a5,a3,a4成等差数列.
(1)求数列{an}的公比;
(2)证明:对任意k∈N+,Sk+2,Sk,Sk+1成等差数列.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第五章第4课时练习卷(解析版) 题型:填空题
一个等差数列前4项之和为26,最末4项之和为110,所有项之和为187,则它的项数为________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第五章第2课时练习卷(解析版) 题型:填空题
(1)等差数列{an}中,Sn是{an}前n项和,已知S6=2,S9=5,则S15=________;
(2)给定81个数排成如图所示的数表,若每行9个数与每列的9个数按表中顺序构成等差数列,且表中正中间一个数a55=5,则表中所有数之和为________.
a11 | a12 | … | a19 |
a21 | a22 | … | a29 |
… | … | … | … |
a91 | a92 | … | a99 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com