
【题目】已知函数f(x)=2sinxcosx-![]() cos2x.
cos2x.
(1)求f(0)的值及函数f(x)的单调递增区间;
(2)求函数f(x)在区间![]() 上的最大值和最小值.
上的最大值和最小值.
【答案】(1)![]() ,k∈Z (2)x=0时,f(x)取得最小值-
,k∈Z (2)x=0时,f(x)取得最小值-![]() ,当2x-
,当2x-![]() =
=![]() ,即x=
,即x=![]() 时,f(x)取得最大值2
时,f(x)取得最大值2
【解析】试题分析(1)先将原式化简为2sin![]() 再令-
再令-![]() +2kπ≤2x-
+2kπ≤2x-![]() ≤
≤![]() +2kπ求出递增区间(2)先求出-
+2kπ求出递增区间(2)先求出-![]() ≤2x-
≤2x-![]() ≤
≤![]() 所以当2x-
所以当2x-![]() =-
=-![]() ,即x=0时,f(x)取得最小值-
,即x=0时,f(x)取得最小值-![]() 当2x-
当2x-![]() =
=![]() ,即x=
,即x=![]() 时,f(x)取得最大值2
时,f(x)取得最大值2
试题解析:
解:(1)因为f(x)=sin2x-![]() cos2x=2sin
cos2x=2sin![]() ,
,
所以f(0)=-![]()
由-![]() +2kπ≤2x-
+2kπ≤2x-![]() ≤
≤![]() +2kπ,k∈Z,
+2kπ,k∈Z,
得-![]() +kπ≤x≤
+kπ≤x≤![]() +kπ,k∈Z,
+kπ,k∈Z,
所以f(x)的单调递增区间是![]() ,k∈Z
,k∈Z
(2)因为0≤x≤![]() ,所以-
,所以-![]() ≤2x-
≤2x-![]() ≤
≤![]()
所以,当2x-![]() =-
=-![]() ,即x=0时,f(x)取得最小值-
,即x=0时,f(x)取得最小值-![]()
当2x-![]() =
=![]() ,即x=
,即x=![]() 时,f(x)取得最大值2
时,f(x)取得最大值2


 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:高中数学 来源: 题型:
【题目】设![]() 实数
实数![]() 满足不等式
满足不等式![]() 函数
函数![]() 无极值点.
无极值点.
(1)若“![]() ”为假命题,“
”为假命题,“![]() ”为真命题,求实数
”为真命题,求实数![]() 的取值范围;
的取值范围;
(2)已知“![]() ”为真命题,并记为
”为真命题,并记为![]() ,且
,且![]() ,若
,若![]() 是
是![]() 的必要不充分条件,求正整数
的必要不充分条件,求正整数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为加强学生的交通安全教育,对学校旁边![]() ,
,![]() 两个路口进行了8天的检测调查,得到每天各路口不按交通规则过马路的学生人数(如茎叶图所示),且
两个路口进行了8天的检测调查,得到每天各路口不按交通规则过马路的学生人数(如茎叶图所示),且![]() 路口数据的平均数比
路口数据的平均数比![]() 路口数据的平均数小2.
路口数据的平均数小2.
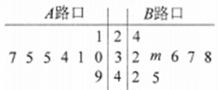
(1)求出![]() 路口8个数据中的中位数和茎叶图中
路口8个数据中的中位数和茎叶图中![]() 的值;
的值;
(2)在![]() 路口的数据中任取大于35的2个数据,求所抽取的两个数据中至少有一个不小于40的概率.
路口的数据中任取大于35的2个数据,求所抽取的两个数据中至少有一个不小于40的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在互联网时代,网校培训已经成为青年学习的一种趋势,假设某网校的套题每日的销售量![]() (单位:千套)与销售价格
(单位:千套)与销售价格![]() (单位:元/套)满足的关系式
(单位:元/套)满足的关系式![]() (
(![]() ,
,![]() 为常数),其中
为常数),其中![]() 与
与![]() 成反比,
成反比,![]() 与
与![]() 的平方成正比,已知销售价格为5元/套时,每日可售出套题21千套,销售价格为3.5元/套时,每日可售出套题69千套.
的平方成正比,已知销售价格为5元/套时,每日可售出套题21千套,销售价格为3.5元/套时,每日可售出套题69千套.
(1) 求![]() 的表达式;
的表达式;
(2) 假设网校的员工工资,办公等所有开销折合为每套题3元(只考虑销售出的套数),试确定销售价格![]() 的值,使网校每日销售套题所获得的利润最大.(保留1位小数)
的值,使网校每日销售套题所获得的利润最大.(保留1位小数)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆x2+y2-6x-8y+21=0和直线kx-y-4k+3=0.
(1)若直线和圆总有两个不同的公共点,求k的取值集合
(2)求当k取何值时,直线被圆截得的弦最短,并求这最短弦的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业共有20条生产线,由于受生产能力和技术水平等因素的影响,会产生一定量的次品.根据经验知道,每台机器产生的次品数![]() 万件与每台机器的日产量
万件与每台机器的日产量![]() 万件
万件![]() 之间满足关系:
之间满足关系: ![]() .已知每生产1万件合格的产品可以以盈利3万元,但每生产1万件次品将亏损1万元.
.已知每生产1万件合格的产品可以以盈利3万元,但每生产1万件次品将亏损1万元.
(Ⅰ)试将该企业每天生产这种产品所获得的利润![]() 表示为
表示为![]() 的函数;
的函数;
(Ⅱ)当每台机器的日产量为多少时,该企业的利润最大,最大为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com