
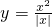
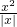 不满足③,从而得出结论.
不满足③,从而得出结论. 在区间(0,1)上大于零,故满足②在区间(0,1)上是增函数.
在区间(0,1)上大于零,故满足②在区间(0,1)上是增函数.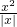 没有最小值,故不满足③,
没有最小值,故不满足③,

 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:高中数学 来源: 题型:单选题
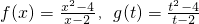
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 ,
, )(m≥0,n≥0).设点,A(1,3),B(3,1),点M是线段AB上一动点,f:M→M′.当点M在线段AB上从点A开始运动到点B结束时,点M的对应点M′所经过的路线长度为________.
)(m≥0,n≥0).设点,A(1,3),B(3,1),点M是线段AB上一动点,f:M→M′.当点M在线段AB上从点A开始运动到点B结束时,点M的对应点M′所经过的路线长度为________.查看答案和解析>>
科目:高中数学 来源: 题型:单选题
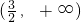

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
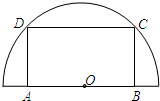 如图,在半径为20cm的半圆形(O为圆心)铝皮上截取一块矩形材料ABCD,其中点A、B在直径上,点C、D在圆周上.
如图,在半径为20cm的半圆形(O为圆心)铝皮上截取一块矩形材料ABCD,其中点A、B在直径上,点C、D在圆周上.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
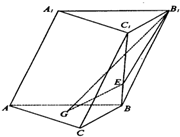 如图,在斜三棱柱ABC-A1B1C1中,侧面AA1B1B⊥底面ABC,侧棱AA1与底面ABC成60° 的角,AA1=2.底面ABC是边长为2的正三角形,其重心为G点,E是线段BC1上一点,且BE=
如图,在斜三棱柱ABC-A1B1C1中,侧面AA1B1B⊥底面ABC,侧棱AA1与底面ABC成60° 的角,AA1=2.底面ABC是边长为2的正三角形,其重心为G点,E是线段BC1上一点,且BE= BC1.
BC1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com