练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知两条不重合的直线和两个不重合的平面，若，则下列四个命题：①若，则；②若，则； ③若，则；④若，则，其中正确命题的个数是（ ）

    A. 0 B. 1 C. 2 D. 3

    【答案】C

    【解析】对于①,若,则,因为,所以,所以①正确;对于②,若时, ,不能推出,所以不能得出,②错误;对于③,若,则,而,由面面垂直的判定定理有,所以③正确;对于④,若,又, ,则的关系不能确定,可能平行,可能相交,可能异面,④错误.正确的有①③,故正确命题的个数为2.选C.

    点睛:本题主要考查了立体几何中的线面位置关系,属于易错题.在①中考查了线面垂直的性质定理,线面垂直,则线线垂直;在②中,反例:见下图,直三棱柱中, 平面, 面,但平面平面,故②是错误的; ③是考查面面垂直的判定定理;在④中, 直线的位置关系不能确定,可能平行,可能相交,可能异面.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】关于二项式(x－1)2 013有下列命题：

    (1)该二项展开式中非常数项的系数和是1；

    (2)该二项展开式中第六项为C2 0136x2 007；

    (3)该二项展开式中系数最大的项是第1 007项；

    (4)当x＝2 014时，(x－1)2 013除以2 014的余数是2 013.

    其中正确命题有(　　)

    A. 1个 B. 2个 C. 3个 D. 4个

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，四棱锥中， ，侧面为等边三角形， ， .

    （Ⅰ）证明： 平面；

    （Ⅱ）求与平面所成的角的大小.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列4个命题：

    ①“若成等比数列，则”的逆命题；

    ②“如果，则”的否命题；

    ③在中，“若”则“”的逆否命题；

    ④当时，若对恒成立，则的取值范围是.

    其中真命题的序号是__________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知点，圆是以的中点为圆心， 为半径的圆.

    （Ⅰ）若圆的切线在轴和轴上截距相等，求切线方程；

    （Ⅱ）若是圆外一点，从向圆引切线， 为切点， 为坐标原点，且有，求使最小的点的坐标.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】袋中有个黄色、个白色的乒乓球，做不放回抽样，每次任取个球，取次，则关于事件“直到第二次才取到黄色球”与事件“第一次取到白球的情况下，第二次恰好取得黄球”的概率说法正确的是（ ）

    A. 事件“直到第二次才取到黄色球”与事件“第一次取得白球的情况下，第二次恰好取得黄球”的概率都等于

    B. 事件“直到第二次才取到黄色球”与事件“第一次取得白球的情况下，第二次恰好取得黄球”的概率都等于

    C. 事件“直到第二次才取到黄色球”的概率等于，事件“第一次取得白球的情况下，第二次恰好取得黄球”的概率等于

    D. 事件“直到第二次才取到黄色球”的概率等于，事件“第一次取得白球的情况下，第二次恰好取得黄球”的概率等于

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆： 的上下两个焦点分别为， ，过点与轴垂直的直线交椭圆于、两点， 的面积为，椭圆的离心力为．

    （Ⅰ）求椭圆的标准方程；

    （Ⅱ）已知为坐标原点，直线： 与轴交于点，与椭圆交于， 两个不同的点，若存在实数，使得，求的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某学校为推行“高效课堂”教学法，某数学老师分别用传统教学和“高效课堂”两种不同的教学方法，在同一年级的甲、乙两个同层次的班进行教学实验，为了解教学效果，期末考试后, 分别从两个班级中各随机抽取20名学生的成绩进行统计，作出的茎叶图如图(记成绩不低于70分者为“成绩优良”).

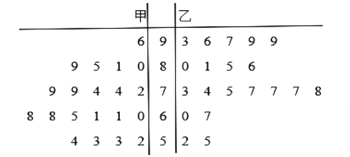
    （1）分别计算甲、乙两班20个样本中，数学成绩前十名的平均分，并大致判断那种教学方法的教学效果更佳；

    （2）由以上统计数据填写下面列联表，并判断能否在犯错误的概率不超过0.05的前提下认为“成绩优良与教学方法有关”？

    附：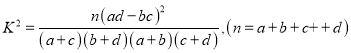

    独立性检验临界表：

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】（本小题满分为14分）已知定义域为R的函数是奇函数．

    （1）求a，b的值；

    （2）若对任意的t∈R，不等式f（t2－2t）＋f（2t2－k）<0恒成立，求k的取值范围．

    查看答案和解析>>

    同步练习册答案