
【题目】下列4个命题:
①“若![]() 成等比数列,则
成等比数列,则![]() ”的逆命题;
”的逆命题;
②“如果![]() ,则
,则![]() ”的否命题;
”的否命题;
③在![]() 中,“若
中,“若![]() ”则“
”则“![]() ”的逆否命题;
”的逆否命题;
④当![]() 时,若
时,若![]() 对
对![]() 恒成立,则
恒成立,则![]() 的取值范围是
的取值范围是![]() .
.
其中真命题的序号是__________.
【答案】②,③
【解析】①“若a、G、b成等比数列,则G2=ab”的逆命题为“若G2=ab,则a、G、b成等比数列”,
不正确,比如a=G=b=0,则a、G、b不成等比数列,故①错;
②“如果x2+x60,则x>2”的否命题为“②“如果x2+x6<0,则x2”的否命题”,
由x2+x6<0,可得3<x<2,推得x2,故②对;
③在△ABC中,“若A>B”“a>b”“2RsinA>2RsinB”“sinA>sinB”(R为外接圆的半径)则其逆否命题正确,故③对;
④当0απ时,若8x2(8sinα)x+cos2α0对x∈R恒成立,即有△=64sin2α32cos2α0,
即有12cos2α0,即为cos2α![]() ,可得
,可得![]() ,
,
解得![]() ,故④错。
,故④错。
故真命题的序号是②③。


 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案科目:高中数学 来源: 题型:
【题目】4月23日是世界读书日,惠州市某中学在此期间开展了一系列的读书教育活动。为了解本校学生课外阅读情况,学校随机抽取了100名学生对其课外阅读时间进行调查。下面是根据调查结果绘制的学生日均课外阅读时间(单位:分钟)的频率分布直方图,且将日均课外阅读时间不低于60分钟的学生称为“读书迷”,低于60分钟的学生称为“非读书迷”.
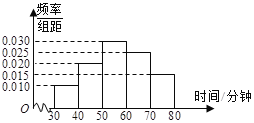
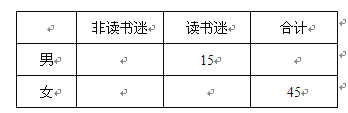
(Ⅰ)根据已知条件完成下面2×2列联表,并据此判断是否有99%的把握认为“读书迷”与性别有关?
(Ⅱ)将频率视为概率,现在从该校大量学生中用随机抽样的方法每次抽取1人,共抽取3次,记被抽取的3人中“读书迷”的人数为![]() ,若每次抽取的结果是相互独立的,求
,若每次抽取的结果是相互独立的,求![]() 的分布列、数学期望
的分布列、数学期望![]() 和方差
和方差![]() .
.
附: 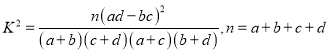
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥![]() 中,
中, ![]() 平面
平面![]() ,底面
,底面![]() 为直角梯形,
为直角梯形, ![]() ,
, ![]() ,
, ![]() ,且
,且![]() 为线段
为线段![]() 上的一动点.
上的一动点.
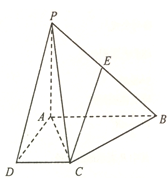
(Ⅰ)若![]() 为线段
为线段![]() 的中点,求证:
的中点,求证: ![]() 平面
平面![]() ;
;
(Ⅱ)当直线![]() 与平面
与平面![]() 所成角小于
所成角小于![]() ,求
,求![]() 长度的取值范围.
长度的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某次水下科研考察活动中,需要潜水员潜入水深为60米的水底进行作业,根据已往经验,潜水员下潜的平均速度为![]() (米/单位时间),每单位时间的用氧量为
(米/单位时间),每单位时间的用氧量为![]() (升),在水底作业10个单位时间,每单位时间用氧量为
(升),在水底作业10个单位时间,每单位时间用氧量为![]() (升),返回水面的平均速度为
(升),返回水面的平均速度为![]() (米/单位时间),每单位时间用氧量为
(米/单位时间),每单位时间用氧量为![]() (升),记该潜水员在此次考察活动中的总用氧量为
(升),记该潜水员在此次考察活动中的总用氧量为![]() (升).
(升).
(1)求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)若![]() ,求当下潜速度
,求当下潜速度![]() 取什么值时,总用氧量最少.
取什么值时,总用氧量最少.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的长轴长为
的长轴长为![]() ,
, ![]() 为坐标原点.
为坐标原点.
(1)求椭圆![]() 的方程和离心率.
的方程和离心率.
(2)设点![]() ,动点
,动点![]() 在
在![]() 轴上,动点
轴上,动点![]() 在椭圆
在椭圆![]() 上,且点
上,且点![]() 在
在![]() 轴的右侧.若
轴的右侧.若![]() ,求四边形
,求四边形![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知城![]() 和城
和城![]() 相距
相距![]() ,现计划以
,现计划以![]() 为直径的半圆上选择一点
为直径的半圆上选择一点![]() (不与点
(不与点![]() ,
, ![]() 重合)建造垃圾处理厂.垃圾处理厂对城市的影响度与所选地点到城市的距离有关,对城
重合)建造垃圾处理厂.垃圾处理厂对城市的影响度与所选地点到城市的距离有关,对城![]() 和城
和城![]() 的总影响度为对城
的总影响度为对城![]() 与城
与城![]() 的影响度之和.记点到
的影响度之和.记点到![]() 城
城![]() 的距离为
的距离为![]() ,建在
,建在![]() 处的垃圾处理厂对城
处的垃圾处理厂对城![]() 和城
和城![]() 的总影响度为
的总影响度为![]() .统计调查表明:垃圾处理厂对城
.统计调查表明:垃圾处理厂对城![]() 的影响度与所选地点到城
的影响度与所选地点到城![]() 的距离的平方成反比例关系,比例系数为4;对城
的距离的平方成反比例关系,比例系数为4;对城![]() 的影响度与所选地点到城
的影响度与所选地点到城![]() 的距离的平方成反比例关系,比例系数为
的距离的平方成反比例关系,比例系数为![]() .当垃圾处理厂建在
.当垃圾处理厂建在![]() 的中点时,对城
的中点时,对城![]() 和城
和城![]() 的总影响度为0.065.
的总影响度为0.065.
(1)将![]() 表示成
表示成![]() 的函数.
的函数.
(2)讨论(1)中函数的单调性,并判断在![]() 上是否存在一点,使建在此处的垃圾处理厂对城
上是否存在一点,使建在此处的垃圾处理厂对城![]() 和城
和城![]() 的总影响度最小?若存在,求出该点到城
的总影响度最小?若存在,求出该点到城![]() 的距离;若不存在,请说明理由.
的距离;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知两条不重合的直线![]() 和两个不重合的平面
和两个不重合的平面![]() ,若
,若![]() ,则下列四个命题:①若
,则下列四个命题:①若![]() ,则
,则![]() ;②若
;②若![]() ,则
,则![]() ; ③若
; ③若![]() ,则
,则![]() ;④若
;④若![]() ,则
,则![]() ,其中正确命题的个数是( )
,其中正确命题的个数是( )
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,以坐标原点![]() 为极点,
为极点, ![]() 轴的非负半轴为极轴建立极坐标系.已知点
轴的非负半轴为极轴建立极坐标系.已知点![]() 的极坐标为
的极坐标为![]() ,曲线
,曲线![]() 的参数方程为
的参数方程为![]() 为参数).
为参数).
(1)直线![]() 过
过![]() 且与曲线
且与曲线![]() 相切,求直线
相切,求直线![]() 的极坐标方程;
的极坐标方程;
(2)点![]() 与点
与点![]() 关于
关于![]() 轴对称,求曲线
轴对称,求曲线![]() 上的点到点
上的点到点![]() 的距离的取值范围.
的距离的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com