
【题目】在四棱锥![]() 中,
中, ![]() 平面
平面![]() ,底面
,底面![]() 为直角梯形,
为直角梯形, ![]() ,
, ![]() ,
, ![]() ,且
,且![]() 为线段
为线段![]() 上的一动点.
上的一动点.
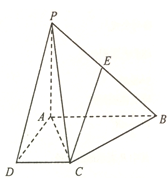
(Ⅰ)若![]() 为线段
为线段![]() 的中点,求证:
的中点,求证: ![]() 平面
平面![]() ;
;
(Ⅱ)当直线![]() 与平面
与平面![]() 所成角小于
所成角小于![]() ,求
,求![]() 长度的取值范围.
长度的取值范围.
【答案】(Ⅰ)证明见解析(Ⅱ)![]()
【解析】试题分析:(1)取PA的中点F,连结EF,DF,证明四边形EFDC是平行四边形得出CE∥DF,故而CE∥平面PAD;
(2)证明BC⊥平面PAC,可知∠PCE为CE与平面PAC所成的角,利用余弦定理得出∠BPC,利用勾股定理得出PE的最大值即可得出PE的范围.
试题解析:
解:(Ⅰ)取![]() 的中点
的中点![]() ,连接
,连接![]() ,∵
,∵![]() 为
为![]() 的中点.
的中点.
∴![]() ,
,
∴四边形![]() 是平行四边形,∴
是平行四边形,∴![]() ,又
,又![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
(Ⅱ)方法一:∵![]() ,∴
,∴![]() ,又
,又![]() ,∴
,∴![]() ,∴
,∴![]() ,又
,又![]() ,∴
,∴![]() 平面
平面![]()
∴![]() 与平面
与平面![]() 所成角就是
所成角就是![]() ,∴
,∴![]() .
.
∵![]() ,∴
,∴![]() ,∴
,∴![]() .
.
∵![]() ,∴
,∴![]() .
.
方法二:以![]() 为坐标原点,以直线
为坐标原点,以直线![]() 为
为![]() 轴,直线
轴,直线![]() 为
为![]() 轴,直线
轴,直线![]() 为
为![]() 轴,
轴,
则![]() ,取线段
,取线段![]() 中点
中点![]() ,则
,则![]() .
.
易得![]() ,所以
,所以![]() 为平面
为平面![]() 的一个法向量.
的一个法向量.
可求得![]() .
.
设![]() ,
, ![]() ,
, ![]() ,
, ![]()
设![]() 与平面
与平面![]() 所成的角
所成的角![]() ,
,
所以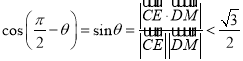 ,
,
化简得![]() ,易得
,易得![]() ,所以
,所以![]() .
.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sinx-![]() cosx+2,记函数f(x)的最小正周期为β,向量a=(2,cosα),b=(1,tan(α+
cosx+2,记函数f(x)的最小正周期为β,向量a=(2,cosα),b=(1,tan(α+![]() ))(0<α<
))(0<α<![]() ),且a·b=
),且a·b=![]() .
.
(1)求f(x)在区间![]() 上的最值;
上的最值;
(2)求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于二项式(x-1)2 013有下列命题:
(1)该二项展开式中非常数项的系数和是1;
(2)该二项展开式中第六项为C2 0136x2 007;
(3)该二项展开式中系数最大的项是第1 007项;
(4)当x=2 014时,(x-1)2 013除以2 014的余数是2 013.
其中正确命题有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知图①②都是表示输出所有立方小于1 000的正整数的程序框图,则图中应分别补充的条件为( )
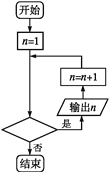
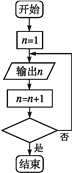
① ②
A. ①n3≥1 000? ②n3<1 000?
B. ①n3≤1 000? ②n3≥1 000?
C. ①n3<1 000? ②n3≥1 000?
D. ①n3<1 000? ②n3<1 000?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从5名男生和4名女生中选出4人去参加座谈会,问:
(1)如果4人中男生和女生各选2人,有多少种选法?
(2)如果男生中的甲与女生中的乙至少要有1人在内,有多少种选法?
(3)如果4人中必须既有男生又有女生,有多少种选法?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列4个命题:
①“若![]() 成等比数列,则
成等比数列,则![]() ”的逆命题;
”的逆命题;
②“如果![]() ,则
,则![]() ”的否命题;
”的否命题;
③在![]() 中,“若
中,“若![]() ”则“
”则“![]() ”的逆否命题;
”的逆否命题;
④当![]() 时,若
时,若![]() 对
对![]() 恒成立,则
恒成立,则![]() 的取值范围是
的取值范围是![]() .
.
其中真命题的序号是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为推行“高效课堂”教学法,某数学老师分别用传统教学和“高效课堂”两种不同的教学方法,在同一年级的甲、乙两个同层次的班进行教学实验,为了解教学效果,期末考试后, 分别从两个班级中各随机抽取20名学生的成绩进行统计,作出的茎叶图如图(记成绩不低于70分者为“成绩优良”).
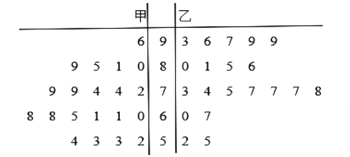
(1)分别计算甲、乙两班20个样本中,数学成绩前十名的平均分,并大致判断那种教学方法的教学效果更佳;
(2)由以上统计数据填写下面![]() 列联表,并判断能否在犯错误的概率不超过0.05的前提下认为“成绩优良与教学方法有关”?
列联表,并判断能否在犯错误的概率不超过0.05的前提下认为“成绩优良与教学方法有关”?

附: 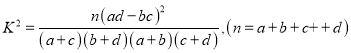
独立性检验临界表:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com