在各项均为正数的等比数列{an}中,已知a2=a1+2,且2a2,a4,3a3成等差数列.
(1)求数列{an}的通项公式;
(2)设bn=log2an,求数列{anbn}的前n项和Sn.
【答案】
分析:(1)利用2a
2,a
4,3a
3成等差数列,a
2=a
1+2,确定数列的公比,从而可求数列{a
n}的通项公式;
(2)确定数列{a
nb
n}的通项,利用错位相减法,即可求数列{a
nb
n}的前n项和S
n.
解答:解:(1)因为2a
2,a
4,3a
3成等差数列,
所以2a
4=2a
2+3a
3,
因为{a
n}为等比数列,所以2a
1q
3=2a
1q+3a
1q
2.
因为a
1≠0,q≠0,所以2q
2-3q-2=0,即(q-2)(2q+1)=0.
因为q>0,所以q=2
因为a
2=a
1+2,所以2a
1=a
1+2,所以a
1=2,
所以a
n=2
n;
(2)b
n=log
2a
n=n,∴a
nb
n=n•2
n∴
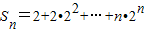
∴
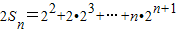
两式相减可得
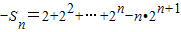
=2
n+1-2-n•2
n+1∴S
n=(n-1)•2
n+1+2.
点评:本题考查等差数列与等比数列的综合,考查数列的通项与求和,考查错位相减法,属于中档题.

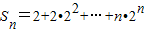
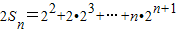
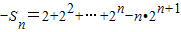 =2n+1-2-n•2n+1
=2n+1-2-n•2n+1
