
【题目】设函数![]() .
.
(1)求![]() 的单调区间;
的单调区间;
(2)若![]() 为整数, 且当
为整数, 且当![]() 时,
时,![]() , 求
, 求![]() 的最大值.
的最大值.
【答案】(1)若![]() ,
,![]() 增区间为
增区间为![]() ,若
,若![]() ,
,![]() 减区间为
减区间为![]() ,增区间为
,增区间为![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)利用导数工具,结合分类讨论思想对![]() 进行分类讨论;(2)由
进行分类讨论;(2)由![]() ,代入原不等式后可将原命题转化为:当
,代入原不等式后可将原命题转化为:当![]() 时,
时, ![]() ,令
,令![]() , 从而原命题可转化为
, 从而原命题可转化为![]()
![]() ,然后利用导数工具求
,然后利用导数工具求![]() .
.
试题解析:(1)函数![]() 的定义域是
的定义域是![]() ,若
,若![]() ,则
,则![]() ,
,
所以函数![]() 在
在![]() 上单调递增.若
上单调递增.若![]() , 则当
, 则当![]() 时,
时,![]() ; 当
; 当![]() 时,
时,![]() ; 所以,
; 所以,![]() 在
在![]() 单调递减,
单调递减,
在![]() 单调递增.
单调递增.
(2)由于![]() ,所以
,所以![]() ,故当
,故当![]() 时,
时, ![]() 等价于
等价于![]() ① 令
① 令![]() ,
,
则 ,由(1)知,当
,由(1)知,当![]() 时, 函数
时, 函数![]() 在
在
![]() 上单调递增, 而
上单调递增, 而![]() 在
在![]() 上存在唯一的零点, 故
上存在唯一的零点, 故
![]() 在
在![]() 上存在唯一的零点, 设此零点为
上存在唯一的零点, 设此零点为![]() ,则有
,则有![]() ,当
,当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ; 所以
; 所以![]() 在
在![]() 上的最小值为
上的最小值为![]() ,又由
,又由![]() ,可得
,可得
![]() ,由于 ①式等价于
,由于 ①式等价于![]() ,故整数
,故整数![]() 的最大值为
的最大值为![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】如图所示,在四棱锥P-ABCD中,底面是边长为1的正方形,侧棱PD=1,PA=PC=![]() .
.
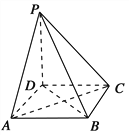
(1)求证:PD⊥平面ABCD;
(2)求证:平面PAC⊥平面PBD;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】校高一(1)班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的污损,可见部分如下图.
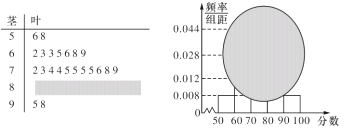
(1)求分数在![]() 的频率及全班人数;
的频率及全班人数;
(2)求分数在![]() 之间的频数,并计算频率分布直方图中
之间的频数,并计算频率分布直方图中![]() 间矩形的高;
间矩形的高;
(3)若要从分数在![]() 之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,至少有一份分数在
之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,至少有一份分数在![]() 之间的概率.
之间的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】围建一个面积为360![]() 的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的进出口,如图所示,已知旧墙的维修费用为45元/m,新墙的造价为180元/m,设利用的旧墙的长度为
的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的进出口,如图所示,已知旧墙的维修费用为45元/m,新墙的造价为180元/m,设利用的旧墙的长度为![]() (单位:
(单位:![]() ),修建此矩形场地围墙的总费用为
),修建此矩形场地围墙的总费用为![]() (单位:元)
(单位:元)
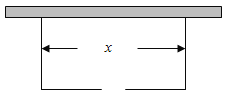
(1)将![]() 表示为
表示为![]() 的函数;
的函数;
(2)试确定![]() ,使修建此矩形场地围墙的总费用最小,并求出最小总费用。
,使修建此矩形场地围墙的总费用最小,并求出最小总费用。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将一颗质地均匀的正方体骰子(六个面的点数分别为1,2,3,4,5,6)先后抛掷两次,记第一次出现的点数为![]() ,第二次出现的点数为
,第二次出现的点数为![]() .
.
(1)求事件“![]() ”的概率;
”的概率;
(2)求事件“![]() ”的概率.
”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学有学生 ![]() 人,其中一年级
人,其中一年级 ![]() 人,二、三年级各
人,二、三年级各 ![]() 人,现要用抽样方法抽取
人,现要用抽样方法抽取 ![]() 人形成样本,将学生按一、二、三年级依次统一编号为
人形成样本,将学生按一、二、三年级依次统一编号为 ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,如果抽得号码有下列四种情况:
,如果抽得号码有下列四种情况:
①![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ;
;
②![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ;
;
③![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ;
;
④![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ;
;
其中可能是由分层抽样得到,而不可能是由系统抽样得到的一组号码为 ![]()
A. ①② B. ②③ C. ①③ D. ①④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)![]() (k>0)
(k>0)
(1)若f(x)>m的解集为{x|x<-3,或x>-2},求不等式5mx2+kx+3>0的解集;
(2)若存在x>3,使得f(x)>1成立,求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解我校高2017级本部和大学城校区的学生是否愿意参加自主招生培训的情况,对全年级2000名高三学生进行了问卷调查,统计结果如下表:
校区 | 愿意参加 | 不愿意参加 |
重庆一中本部校区 | 220 | 980 |
重庆一中大学城校区 | 80 | 720 |
(1)若从愿意参加自主招生培训的同学中按分层抽样的方法抽取15人,则大学城校区应抽取几人;
(2)现对愿意参加自主招生的同学组织摸底考试,考试题共有5道题,每题20分,对于这5道题,考生“如花姐”完全会答的有3题,不完全会的有2道,不完全会的每道题她得分![]() 的概率满足:
的概率满足:![]() ,假设解答各题之间没有影响,
,假设解答各题之间没有影响,
①对于一道不完全会的题,求“如花姐”得分的均值![]() ;
;
②试求“如花姐”在本次摸底考试中总得分的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市随机抽取一年(365天)内100天的空气质量指数![]() 的检测数据,结果统计如下:
的检测数据,结果统计如下:
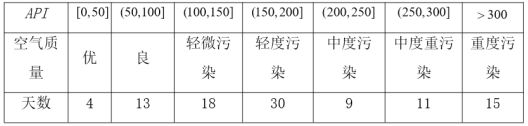
记某企业每天由空气污染造成的经济损失![]() (单位:元),空气质量指数
(单位:元),空气质量指数![]() 为
为![]() .在区间
.在区间![]() 对企业没有造成经济损失;在区间
对企业没有造成经济损失;在区间![]() 对企业造成经济损失成直线模型(当
对企业造成经济损失成直线模型(当![]() 为150时造成的经济损失为500元,当
为150时造成的经济损失为500元,当![]() 为200时,造成的经济损失为700元);当
为200时,造成的经济损失为700元);当![]() 大于300时造成的经济损失为2000元.
大于300时造成的经济损失为2000元.
(1)试写出![]() 的表达式;
的表达式;
(2)试估计在本年内随机抽取一天,该天经济损失![]() 大于200元且不超过600元的概率;
大于200元且不超过600元的概率;
(3)若本次抽取的样本数据有30天是在供暖季,其中有8天为重度污染,完成下面![]() 列联表,并判断
列联表,并判断
能否有![]() 的把握认为该市本年空气重度污染与供暖有关?
的把握认为该市本年空气重度污染与供暖有关?
附:
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 1.32 | 2.07 | 2.70 | 3.74 | 5.02 | 6.63 | 7.87 | 10.82 |
![]()
非重度污染 | 重度污染 | 合计 | |
供暖季 | |||
非供暖季 | |||
合计 | 100 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com