
【题目】已知函数f(x)=x2+2xsinθ﹣1,x∈[﹣ ![]() ,
, ![]() ].
].
(1)当 ![]() 时,求函数f(x)的最小值;
时,求函数f(x)的最小值;
(2)若函数f(x)在x∈[﹣ ![]() ,
, ![]() ]上是单调增函数,且θ∈[0,2π],求θ的取值范围.
]上是单调增函数,且θ∈[0,2π],求θ的取值范围.
【答案】
(1)解:当θ= ![]() 时,f(x)=x2+x﹣1=(x+
时,f(x)=x2+x﹣1=(x+ ![]() )2﹣
)2﹣ ![]() ,
,
由于x∈[﹣ ![]() ,
, ![]() ],故当x=﹣
],故当x=﹣ ![]() 时,f(x)有最小值﹣
时,f(x)有最小值﹣ ![]() ;
;
当x= ![]() 时,f(x)有最大值﹣
时,f(x)有最大值﹣ ![]() .
.
(2)解:因为f(x)=x2+2xsinθ﹣1的对称轴为x=﹣sinθ,
又欲使f(x)在区间[﹣ ![]() ,
, ![]() ]上是单调函数,
]上是单调函数,
则﹣sinθ≤﹣ ![]() ,或﹣sinθ≥
,或﹣sinθ≥ ![]() ,即sinθ≥
,即sinθ≥ ![]() 或sinθ≤﹣
或sinθ≤﹣ ![]()
因为θ∈[0,2π],
故所求θ的范围是[ ![]() ,
, ![]() ]∪[
]∪[ ![]() ,
, ![]() ].
].
【解析】(1)当θ= ![]() 时,f(x)=x2+x﹣1=(x+
时,f(x)=x2+x﹣1=(x+ ![]() )2+
)2+ ![]() ,利用二次函数的性质求得f(x)的最大值和最小值.(2)利用f(x)=x2+2xsinθ﹣1的对称轴为x=﹣sinθ,由题意可得﹣sinθ≤﹣
,利用二次函数的性质求得f(x)的最大值和最小值.(2)利用f(x)=x2+2xsinθ﹣1的对称轴为x=﹣sinθ,由题意可得﹣sinθ≤﹣ ![]() ,或﹣sinθ≥
,或﹣sinθ≥ ![]() ,求得sinθ的范围,再结合θ的范围,确定出θ的具体范围.
,求得sinθ的范围,再结合θ的范围,确定出θ的具体范围.
【考点精析】关于本题考查的利用导数研究函数的单调性,需要了解一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减才能得出正确答案.
在这个区间单调递减才能得出正确答案.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin(ωx+φ)(ω>0,|φ|< ![]() )的部分图象如图所示,则y=f(x)的图象可由y=cos2x图象( )
)的部分图象如图所示,则y=f(x)的图象可由y=cos2x图象( ) 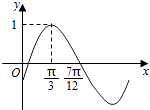
A.向右平移 ![]() 个长度单位
个长度单位
B.向左平移 ![]() 个长度单位
个长度单位
C.向右平移 ![]() 个长度单位
个长度单位
D.向左平移 ![]() 个长度单位
个长度单位
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆W: ![]() ,过原点O作直线l1交椭圆W于A,B两点,P为椭圆上异于A,B的动点,连接PA,PB,设直线PA,PB的斜率分别为k1 , k2(k1 , k2≠0),过O作直线PA,PB的平行线l2 , l3 , 分别交椭圆W于C,D和E,F.
,过原点O作直线l1交椭圆W于A,B两点,P为椭圆上异于A,B的动点,连接PA,PB,设直线PA,PB的斜率分别为k1 , k2(k1 , k2≠0),过O作直线PA,PB的平行线l2 , l3 , 分别交椭圆W于C,D和E,F.
(1)若A,B分别为椭圆W的左、右顶点,是否存在点P,使∠APB=90°?说明理由.
(2)求k1k2的值;
(3)求|CD|2+|EF|2的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知指数函数y=g(x)满足:g(3)=8,定义域为R的函数f(x)= ![]() 是奇函数.
是奇函数.
(1)确定y=g(x),y=f(x)的解析式;
(2)若h(x)=f(x)+a在(﹣1,1)上有零点,求a的取值范围;
(3)若对任意的t∈(﹣4,4),不等式f(6t﹣3)+f(t2﹣k)<0恒成立,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种产品特约经销商根据以往当地的需求情况,得出如图该种产品日需求量的频率分布直方图. 
(1)求图中a的值,并估计日需求量的众数;
(2)某日,经销商购进130件该种产品,根据近期市场行情,当天每售出1件能获利30元,未售出的部分,每件亏损20元.设当天的需求量为x件(100≤x≤150),纯利润为S元.
(ⅰ)将S表示为x的函数;
(ⅱ)根据直方图估计当天纯利润S不少于3400元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x+ ![]() 是奇函数.
是奇函数.
(1)若点Q(1,3)在函数f(x)的图象上,求函数f(x)的解析式;
(2)写出函数f(x)的单调区间(不要解答过程,只写结果);
(3)设点A(t,0),B(t+1,0)(t∈R),点P在f(x)的图象上,且△ABP的面积为2,若这样的点P恰好有4个,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,圆M的方程为x2+y2﹣8x﹣2y+16=0,若直线kx﹣y+3=0上至少存在一点,使得以该点为圆心,半径为1的圆与圆M有公共点,则k的取值范围是( )
A.(﹣∞, ![]() ]
]
B.[0,+∞)
C.[﹣ ![]() ,0]
,0]
D.(﹣∞, ![]() ]∪[0,+∞)
]∪[0,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是某电视台综艺节目举办的挑战主持人大赛上,七位评委为某选手打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( ) 
A.84,4.84
B.84,1.6
C.85,4
D.85,1.6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com