
【题目】已知 ![]() 且满足不等式
且满足不等式 ![]() .
.
(1)求不等式 ![]() ;
;
(2)若函数 ![]() 在区间
在区间 ![]() 有最小值为
有最小值为 ![]() ,求实数
,求实数 ![]() 值.
值.
【答案】
(1)解:∵22a+1>25a-2.
∴2a+1>5a-2,即3a<3
∴a<1,
∵a>0,a<1
∴0<a<1.
∵loga(3x+1)<loga(7-5x).
∴等价为 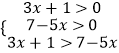 , 即
, 即 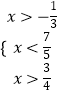 , ∴
, ∴ ![]() ,
,
即不等式的解集为( ![]() ,
, ![]() )
)
(2)解:∵0<a<1
∴函数y=loga(2x-1)在区间[3,6]上为减函数,
∴当x=6时,y有最小值为-2, 即loga11=-2,
∴a-2= ![]() =11, 解得a=
=11, 解得a= ![]()
【解析】(1)先求出a的取值范围,再根据对数函数的图象和性质,可得函数单调递减且3x+1>0,75x>0,3x+1>75x同时成立,解方程组即可得到x的范围。
(2)根据对数函数的单调性和最值,可知在x=6时取得最小值-2,代入再进行指对互换,即可求得a的值。


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+2xsinθ﹣1,x∈[﹣ ![]() ,
, ![]() ].
].
(1)当 ![]() 时,求函数f(x)的最小值;
时,求函数f(x)的最小值;
(2)若函数f(x)在x∈[﹣ ![]() ,
, ![]() ]上是单调增函数,且θ∈[0,2π],求θ的取值范围.
]上是单调增函数,且θ∈[0,2π],求θ的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在数列{an}中,a3=12,a11=﹣5,且任意连续三项的和均为11,则a2017=;设Sn是数列{an}的前n项和,则使得Sn≤100成立的最大整数n= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在等腰梯形ABCD中,AB∥CD,且|AB|=2,|AD|=1,|CD|=2x其中x∈(0,1),以A,B为焦点且过点D的双曲线的离心率为e1 , 以C,D为焦点且过点A的椭圆的离心率为e2 , 若对任意x∈(0,1)不等式t<e1+e2恒成立,则t的最大值为( )
A.![]()
B.![]()
C.2
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某企业生产的某种产品中抽取100件样本,测量这些样本的一项质量指标值,由测量结果得如下频数分布表:
质量指标 | [75,85) | [85,95) | [95,105) | [105,115) | [115,125] |
频数 | 6 | 26 | 38 | 22 | 8 |
则样本的该项质量指标值落在[105,125]上的频率为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD的底面是直角梯形,AB∥CD,AB⊥AD,△PAB和△PAD是两个边长为2的正三角形,DC=4,O为BD的中点. 
(1)求证:PO⊥平面ABCD;
(2)若E为线段PA上一点,且 ![]() ,求二面角P﹣OE﹣C的余弦值.
,求二面角P﹣OE﹣C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直四棱柱 ![]() 中,底面
中,底面 ![]() 是边长为2的正方形,
是边长为2的正方形, ![]() 分别为线段
分别为线段 ![]() ,
, ![]() 的中点.
的中点.
(1)求证: ![]() ||平面
||平面 ![]() ;
;
(2)四棱柱 ![]() 的外接球的表面积为
的外接球的表面积为 ![]() ,求异面直线
,求异面直线 ![]() 与
与 ![]() 所成的角的大小.
所成的角的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com