
| A. | $\frac{13}{15}$ | B. | $\frac{2}{81}$ | C. | $\frac{13}{243}$ | D. | $\frac{80}{243}$ |
分析 X~B(n,$\frac{1}{3}$),若D(x)=$\frac{4}{3}$,则n$•\frac{1}{3}•\frac{2}{3}$=$\frac{4}{3}$,求出n,表示6次独立重复试验,每次实验成功概率为$\frac{1}{3}$,P(X=2)表示6次试验中成功两次的概率.
解答 解:由题意,X~B(n,$\frac{1}{3}$),若D(x)=$\frac{4}{3}$,则n$•\frac{1}{3}•\frac{2}{3}$=$\frac{4}{3}$,∴n=6.
P(X=2)=${C}_{6}^{2}•(\frac{1}{3})^{2}(\frac{2}{3})^{4}$=$\frac{80}{243}$.
故选D.
点评 本题考查独立重复试验中事件的概率及二项分布知识,属基本题.


科目:高中数学 来源: 题型:选择题
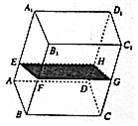 如图,在透明塑料制成的长方体ABCD-A1B1C1D1容器内灌进一些水,将容器底面一边BC固定于地面上,再将容器倾斜,随着倾斜度的不同,有下列四个说法:
如图,在透明塑料制成的长方体ABCD-A1B1C1D1容器内灌进一些水,将容器底面一边BC固定于地面上,再将容器倾斜,随着倾斜度的不同,有下列四个说法:| A. | ②③④ | B. | ①②④ | C. | ①③④ | D. | ①②③ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不必要也不充分条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
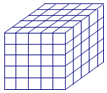 如图,将一个各面都涂了油漆的正方体,切割为125个同样大小的小正方体,经过搅拌后,从中随机取一个小正方体,记它的涂漆面数为X,则X的均值E(X)=$\frac{6}{5}$.
如图,将一个各面都涂了油漆的正方体,切割为125个同样大小的小正方体,经过搅拌后,从中随机取一个小正方体,记它的涂漆面数为X,则X的均值E(X)=$\frac{6}{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 0个或者2个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
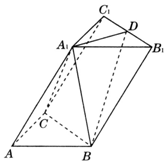 如图,在三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=2,A1A=4,A1在底面ABC的射影为BC的中点,D是B1C1的中点.
如图,在三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=2,A1A=4,A1在底面ABC的射影为BC的中点,D是B1C1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{6}}{3π}$ | B. | $\frac{\sqrt{6}}{6π}$ | C. | $\frac{3\sqrt{2}}{8π}$ | D. | $\frac{3\sqrt{2}}{4π}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com