
����Ŀ��ij���ʳ������ס������ֻ�Ϸ��ϣ���ҪA��B��C������Ҫԭ��.����1��Ƥ���ַ��Ϻ�����1��Ƥ���ַ�����������ԭ�ϵĶ������±���ʾ��
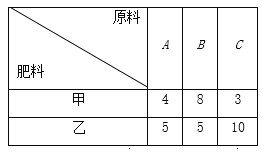
����A��ԭ��200�֣�B��ԭ��360�֣�C��ԭ��300��.�ڴ˻����������ס������ַ���.��֪����1��Ƥ���ַ��ϣ�����������Ϊ2��Ԫ������1��Ƥ���ַ��ϣ�����������Ϊ3��Ԫ.�ֱ���x��y��ʾ�ƻ������ס������ַ��ϵij�Ƥ��.
(1)��x��y�г�����������������ѧ��ϵʽ����������Ӧ��ƽ������
(2)�ʷֱ������ס������ַ��ϸ����ٳ�Ƥ���ܹ�������������������������.
���𰸡���1�������������2���������ַ��� ![]() ��Ƥ�����ַ���
��Ƥ�����ַ��� ![]() ��Ƥʱ����������������Ϊ
��Ƥʱ����������������Ϊ ![]() ��Ԫ.
��Ԫ.
��������
�����������������������ʽ��ϵ����������������
���������Ŀ�꺯��������ƽ��ֱ�߷�������⼴�ɣ�
��1�� ����֪��![]() ��
��![]() �������ѧ��ϵʽΪ
�������ѧ��ϵʽΪ 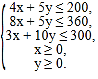
�ö�Ԫһ�β���ʽ������ʾ��ƽ������Ϊͼ1�е���Ӱ���֣�
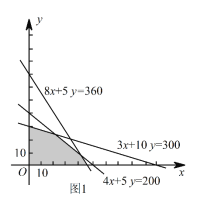
��2�� ������Ϊ ![]() ��Ԫ����Ŀ�꺯��Ϊ
��Ԫ����Ŀ�꺯��Ϊ ![]() ��
��
���� ![]() ����������Ϊ
����������Ϊ ![]() ������б��Ϊ
������б��Ϊ ![]() ����
���� ![]() �仯��һ��ƽ��ֱ�ߣ�
�仯��һ��ƽ��ֱ�ߣ� ![]() Ϊֱ����
Ϊֱ���� ![]() ���ϵĽؾ࣬��
���ϵĽؾ࣬�� ![]() ȡ���ֵʱ��
ȡ���ֵʱ��![]() ��ֵ�������Ϊ
��ֵ�������Ϊ ![]() ��
��![]() ����Լ��������������ͼ2��֪����ֱ��
����Լ��������������ͼ2��֪����ֱ�� ![]() �����������ϵĵ�
�����������ϵĵ� ![]() ʱ���ؾ�
ʱ���ؾ� ![]() ���
��� ![]() ���
���
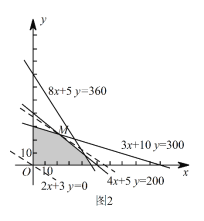
�ⷽ���� ![]() �õ�
�õ� ![]() ������Ϊ
������Ϊ ![]() ��
��
���� ![]() ��
��
���������ַ��� ![]() ��Ƥ�����ַ���
��Ƥ�����ַ��� ![]() ��Ƥʱ����������������Ϊ
��Ƥʱ����������������Ϊ ![]() ��Ԫ��
��Ԫ��


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() ��
��![]() ��������
��������![]() ������
������![]() ��
��![]() �ϵ����ݼ�������
�ϵ����ݼ�������![]() ��������ʵ��
��������ʵ��![]() ������ʽ
������ʽ![]() �����.
�����.
��1��д������![]() �ķ������
�ķ������![]() Ϊ��ʱ��ʵ��
Ϊ��ʱ��ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��2��������⡰![]() ��Ϊ�����⣬�ҡ�
��Ϊ�����⣬�ҡ�![]() ��Ϊ�����⣬��ʵ��
��Ϊ�����⣬��ʵ��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ����һ��ٰ�������ȫ֪ʶ�������ֱ�ѡ��3��������3��Ů������жӺ�Ů�ӣ�ÿ��һ���ش��⣬�����Ϊ���ӵ�10�֣�����벻��0�֣���֪�ж�ÿ�˴�Եĸ�������Ϊ ![]() ��
�� ![]() ��
�� ![]() ��Ů��ÿ�˴�Եĸ��ʶ���
��Ů��ÿ�˴�Եĸ��ʶ��� ![]() ����ÿ�˻ش���ȷ����֮��û��Ӱ�죬��X��ʾ�жӵ��ܵ÷֣�
����ÿ�˻ش���ȷ����֮��û��Ӱ�죬��X��ʾ�жӵ��ܵ÷֣�
��I�� ��X�ķֲ��м�����ѧ����E��X����
���������жӺ�Ů�ӵ÷�֮��Ϊ50�������£��жӱ�Ů�ӵ÷ָߵĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���� ![]() ���ļ�����ƥ���˶��Ὣ��2016��8��5��
���ļ�����ƥ���˶��Ὣ��2016��8��5�� ![]() 21���ڰ�����Լ����¬���У��±��ǽ������˻��й������źͶ���˹�����Ż�õĽ�������ͳ�����ݣ���λ��ö����
21���ڰ�����Լ����¬���У��±��ǽ������˻��й������źͶ���˹�����Ż�õĽ�������ͳ�����ݣ���λ��ö����
�� | ��31����Լ | ��30���� | ��29�챱�� | ��28���ŵ� | ��27��Ϥ�� |
�й� | 26 | 38 | 51 | 32 | 28 |
����˹ | 19 | 24 | 24 | 27 | 32 |
��1�����ݱ���������������ɽ������˻����������Ż�õĽ������ľ�Ҷͼ����ͨ����Ҷͼ�Ƚ����������Ż�õĽ�������ƽ��ֵ����ɢ�̶ȣ���Ҫ������������ֵ���������ۼ��ɣ���
��2���±��ǽ������˻��й������Ż�õĽ�����֮�� ![]() ���ӵ�
���ӵ� ![]() �����𣬲�����֮ǰ�ѻ�õĽ���������ʱ��
�����𣬲�����֮ǰ�ѻ�õĽ���������ʱ�� ![]() ��ʱ����ţ��仯�����ݣ�
��ʱ����ţ��仯�����ݣ�
�� | 27 | 28 | 29 | 30 | 31 |
ʱ�����(x) | 1 | 2 | 3 | 4 | 5 |
������֮��(yö) | 28 | 60 | 111 | 149 | 175 |
����ɢ��ͼ���£�
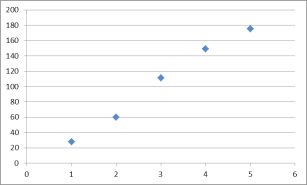
����ͼ�п��Կ�����������֮�� ![]() ��ʱ�����
��ʱ����� ![]() ֮�����������ع�ϵ�������
֮�����������ع�ϵ������� ![]() ����
���� ![]() �����Իع鷽�̣�
�����Իع鷽�̣�
�����â��еĻع鷽�̣�Ԥ��2020���32�����ƥ���˶����й������Ż�õĽ�������
�ο����ݣ�![]() ��
��![]() ��
��![]() ��
��
��������һ������ ![]() ��
��![]() ��
��![]() ��
��![]() ����ع�ֱ��
����ع�ֱ��![]() ��б�ʵ���С���˹���Ϊ
��б�ʵ���С���˹���Ϊ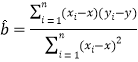 ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ�ij����ͼ���㷨˼·Դ���ҹ��Ŵ���ѧ�е��ؾ����㷨��ִ�иó����ͼ��������Ľ��S��ʾ��ֵΪ�� �� 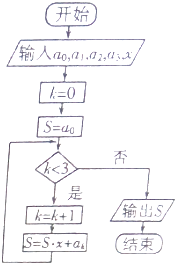
A.a0+a1+a2+a3
B.��a0+a1+a2+a3��x3
C.a0+a1x+a2x2+a3x3
D.a0x3+a1x2+a2x+a3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() .
.
��1����![]() ʱ����
ʱ����![]() ������
������![]() �ϵ���ֵ��
�ϵ���ֵ��
��2�����ۺ���![]() �ĵ����ԣ�
�ĵ����ԣ�
��3����![]() ʱ����
ʱ����![]() ���������
���������![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ![]() �ķ���Ϊ
�ķ���Ϊ![]() �����䳤�᳤Ϊ__________����
�����䳤�᳤Ϊ__________����![]() Ϊ
Ϊ![]() ���ҽ��㣬
���ҽ��㣬 ![]() Ϊ
Ϊ![]() ���϶��㣬
���϶��㣬 ![]() Ϊ
Ϊ![]() ��λ�ڵ�һ�����ڵĶ��㣬���ı���
��λ�ڵ�һ�����ڵĶ��㣬���ı���![]() ����������ֵΪ__________��
����������ֵΪ__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����{an}��ǰn���ΪSn �� ��Sn=n2+2n������{bn}�ǹ��ȴ���1�ĵȱ����У�������b1+b4=9��b2b3=8��
���ֱ�������{an}��{bn}��ͨ�ʽ��
������cn=����1��nSn+anbn �� ������{cn}��ǰn���Tn ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ͼ��ʾ�ij����ͼ��������Ľ���ǣ� �� 
A.e2016��e2015
B.e2017��e2016
C.e2015��1
D.e2016��1
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com