练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】椭圆，椭圆上一点到左焦点的距离的取值范围为.

    （1）求椭圆的方程；

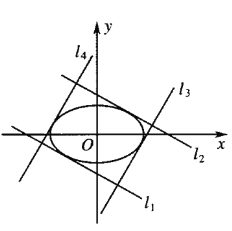
    （2），，，分别与椭圆相切，且，，，如图，，，，围成的矩形的面积记为，求的取值范围.

    【答案】（1）（2）

    【解析】

    （1）根据椭圆的左、右顶点到椭圆的左焦点的距离分别为最小值和最大值列出方程组，求解即可；

    （2）联立直线与椭圆的方程得到一元二次方程，根据韦达定理结合矩形的面积公式得到面积的表达式，结合基本不等式求解面积的取值范围.

    （1）因为椭圆上一点到左焦点的距离的取值范围是，

    设椭圆的焦距为，所以解得

    所以，故椭圆的方程为.

    （2）当，轴或，轴时，；

    当，，，斜率都存在时，设，，，，

    其中，且，.

    将直线的方程与椭圆方程联立得

    ∴.

    由，得，∴，同理可得

    ∵，，

    ∴

    .

    ∵，∴，

    ∴，当且仅当时，等号成立，

    ∴

    ∴，

    综上，

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中，曲线C的参数方程为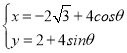（θ为参数），直线l的参数方程为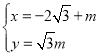（m为参数），以平面直角坐标系的原点O为极点，x轴正半轴为极轴，建立坐标系．

    （1）求曲线C的极坐标方程；

    （2）直线l与曲线C相交于M，N两点，若，求的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列关于函数的叙述正确的为( )

    A.函数有三个零点

    B.点(1，0)是函数图象的对称中心

    C.函数的极大值点为

    D.存在实数a，使得函数为增函数

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知A，B是抛物线上的两点，且在x轴两侧，若AB的中点为Q，分别过A，B两点作T的切线，且两切线相交于点P.

    （1）求证：直线PQ平行于x轴；

    （2）若直线AB经过抛物线T的焦点，求面积的最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】2020年春季，某出租汽车公司决定更换一批新的小汽车以代替原来报废的出租车，现有采购成本分别为万元/辆和万元/辆的两款车型，根据以往这两种出租车车型的数据，得到两款出租车车型使用寿命频数表如下：

    使用寿命年数

    5年

    6年

    7年

    8年

    总计

    型出租车(辆)

    10

    20

    45

    25

    100

    型出租车(辆)

    15

    35

    40

    10

    100

    （1）填写下表，并判断是否有的把握认为出租车的使用寿命年数与汽车车型有关？

    使用寿命不高于年

    使用寿命不低于年

    总计

    型

    型

    总计

    （2）从和的车型中各随机抽取车，以表示这车中使用寿命不低于年的车数，求的分布列和数学期望；

    （3）根据公司要求，采购成本由出租公司负责，平均每辆出租车每年上交公司万元，其余维修和保险等费用自理.假设每辆出租车的使用寿命都是整数年，用频率估计每辆出租车使用寿命的概率，分别以这辆出租车所产生的平均利润作为决策依据，如果你是该公司的负责人，会选择采购哪款车型？

    附：，.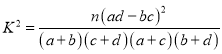

    0.050

    0.010

    0.001

    3.841

    6.635

    10.828

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】党的十九大明确把精准脱贫作为决胜全面建成小康社会必须打好的三大攻坚战之一，为坚决打赢脱贫攻坚战，某帮扶单位考察了甲乙两种不同的农产品加工生产方式，现对两种生产方式加工的产品质量进行测试并打分对比，得到如下数据：

    生产方式甲

    分值区间

    频数

    20

    30

    100

    40

    10

    生产方式乙

    分值区间

    频数

    25

    35

    60

    50

    30

    其中产品质量按测试指标可划分为：指标在区间上的为特优品，指标在区间上的为一等品，指标在区间上的为二等品．

    （1）用事件表示“按照生产方式甲生产的产品为特优品”，估计的概率；

    （2）填写下面列联表，并根据列联表判断能否有的把握认为“特优品”与生产方式有关？

    特优品

    非特优品

    生产方式甲

    生产方式乙

    （3）根据打分结果对甲乙两种生产方式进行优劣比较．

    附表：

    0.10

    0.050

    0.010

    0.001

    2.706

    3.841

    6.635

    10.828

    参考公式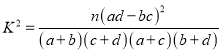：，其中．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数在上的最大值为.

    （1）求的解析式；

    （2）讨论的零点的个数.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】我国古代数学典籍《九章算术》第七章“盈不足”中有一道两鼠穿墙问题：有厚墙尺，两只老鼠从墙的两边相对分别打洞穿墙大老鼠第一天进一尺，以后每天加倍；小老鼠第一天也进一尺，以后每天减半．问两天后，两鼠间距_______尺，两鼠相遇时，大鼠共穿了______尺墙．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】△ABC的内角A，B，C的对边分别为a，b，c，已知2a＝2bcosC+csinB．

    （Ⅰ）求tanB；

    （Ⅱ）若C，△ABC的面积为6，求BC．

    查看答案和解析>>

    同步练习册答案