
如图,矩形ABCD中,AB=6,BC=2![]() ,沿对角线BD将DABC向上折起,使点A移至点P,且P在平面BCD的射影O在DC上.
,沿对角线BD将DABC向上折起,使点A移至点P,且P在平面BCD的射影O在DC上.
(1)求证:PD^PC;
(2)求二面角P-DB-C的平面角的余弦值;
(3)求直线CD与平面PBD所成角的正弦值.
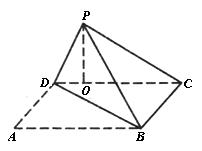
解:(1)∵ PO^平面BCD,DC^BC,PD在底面BCD上的射影为DC,∴ PD^BC. 又PD^PB,PB∩PC=P,∴ PD^平面PBC,PCÌ平面PBC ∴ PD^PC. (2)过P作PN^BD于N连结NO. ∵ PO^平面BDC,∴ PO^BD,∴ BD^平面PNO, ∴ ÐPNO就是二面角P-BD-C的平面角,且ÐPON是直角. RtDPDB中,PD=2 ∴ ÐPBD=30°,∴ PN= RtDPDC中,PD=2 ∴ (3)过O作OM^PN于点M,连DM,∵ BD^平面PNO,∴ OM^BD,∴ OM^平面PDB.∴ ÐODM就是直线DC与平面PDB所成的角.RtDPON中,OM=PO×sinÐNPO=PO× cosÐPNO=PO×cosÐPNO= ∴ ÐBDC=30°,∴ DO=2ON=2,∴ |


科目:高中数学 来源: 题型:
 如图,矩形ABCD中,AB=
如图,矩形ABCD中,AB=8
| ||
| 3 |
| 2π |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 A 若方程ax-x-a=0有两个实数解,则a的取值范围是
A 若方程ax-x-a=0有两个实数解,则a的取值范围是| AE |
| AF |
| 9 |
| 2 |
| 9 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,矩形ABCD中,DC=
如图,矩形ABCD中,DC=| 3 |
2
| ||||
| 12 |
2
| ||||
| 12 |
| 3 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (理)如图,矩形ABCD中,AB=1,BC=a,PA⊥平面ABCD
(理)如图,矩形ABCD中,AB=1,BC=a,PA⊥平面ABCD| PQ |
| QD |
| BP |
| QD |
| ||
| 10 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com