
我们将具有下列性质的所有函数组成集合M:函数y=f(x)(x∈D),对任意x,y,![]() ∈D均满足f(
∈D均满足f(![]() )≥
)≥![]() [f(x)+f(y)],当且仅当x=y时等号成立.
[f(x)+f(y)],当且仅当x=y时等号成立.
(1)若定义在(0,+∞)上的函数f(x)∈M,试比较f(3)+f(5)与2f(4)的大小.
(2)设函数g(x)=-x2,求证:g(x)∈M.
科目:高中数学 来源: 题型:
| x+y |
| 2 |
| x+y |
| 2 |
| 1 |
| 2 |
| 1 |
| x |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x+y |
| 2 |
| x+y |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
我们将具有下列性质的所有函数组成集合M:函数![]() ,对任意
,对任意![]() 均满足
均满足![]() ,当且仅当
,当且仅当![]() 时等号成立。
时等号成立。
(1)若定义在(0,+∞)上的函数![]() ∈M,试比较
∈M,试比较![]() 与
与![]() 大小.
大小.
(2)设函数g(x)=-x2,求证:g(x)∈M.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
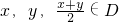 均满足
均满足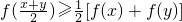 ,当且仅当x=y时等号成立.
,当且仅当x=y时等号成立.查看答案和解析>>
科目:高中数学 来源:2011-2012学年江西省新余市新钢中学高三(上)第二次月考数学试卷(理科)(解析版) 题型:解答题
 均满足
均满足 ,当且仅当x=y时等号成立.
,当且仅当x=y时等号成立. ,f2(x)=logax(a>1,x>0).证明:f1(x)∉M,f2(x)∈M.
,f2(x)=logax(a>1,x>0).证明:f1(x)∉M,f2(x)∈M.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com