已知△ABC的顶点A为(3,-1),AB边上的中线所在直线方程为6x+10y-59=0,∠B的平分线所在直线方程为x-4y+10=0,
(1)求B点的坐标;
(2)求A点关于直线x-4y+10=0对称点A'的坐标;
(3)求BC边所在直线的方程.
解:(1)设B(4y
1-10,y
1),…(1分)
由AB中点(
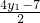
,
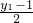
) 在6x+10y-59=0上,可得:6•
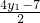
+10•
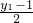
-59=0,解得 y
1=5,
所以B(10,5).…(4分)
(2)设A点关于x-4y+10=0的对称点为 A′(x′,y′),…(5分)
则由
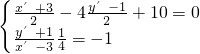
,解得
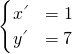
,故A′(1,7).…(8分)
(3)∵A点关于直线x-4y+10=0对称点A'在直线BC上,
∴直线BA'就是直线BC,由两点式可得
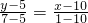
,
化简得BC的方程为2x+9y-65=0.…(12分)
分析:(1)设B(4y
1-10,y
1),由AB中点(
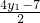
,
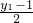
) 在6x+10y-59=0上,求出 y
1=5,即可得到B点的坐标.
(2)设A点关于x-4y+10=0的对称点为 A′(x′,y′),由
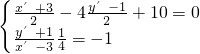
,解得A′的坐标.
(3)A点关于直线x-4y+10=0对称点A'在直线BC上,直线BA'就是直线BC,由两点式求得BC的方程.
点评:本题主要考查求一个点关于直线的对称点的坐标,角平分线的性质的应用,用两点式求直线的方程,属于中档题.

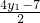 ,
,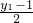 ) 在6x+10y-59=0上,可得:6•
) 在6x+10y-59=0上,可得:6•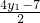 +10•
+10•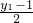 -59=0,解得 y1=5,
-59=0,解得 y1=5,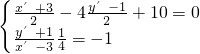 ,解得
,解得 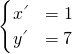 ,故A′(1,7).…(8分)
,故A′(1,7).…(8分)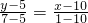 ,
,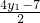 ,
,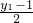 ) 在6x+10y-59=0上,求出 y1=5,即可得到B点的坐标.
) 在6x+10y-59=0上,求出 y1=5,即可得到B点的坐标.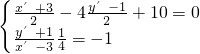 ,解得A′的坐标.
,解得A′的坐标.
