
【题目】以原点O为极点,x轴的正半轴为极轴建立极坐标系,直线l的方程为 ![]() ,⊙C的极坐标方程为ρ=4cosθ+2sinθ.
,⊙C的极坐标方程为ρ=4cosθ+2sinθ.
(1)求直线l和⊙C的普通方程;
(2)若直线l与圆⊙C交于A,B两点,求弦AB的长.
【答案】
(1)解:直线l的方程为 ![]() ,
,
可得:ρsinθcos ![]() ﹣ρcosθsin
﹣ρcosθsin ![]() =﹣
=﹣ ![]()
﹣ ![]() y﹣
y﹣ ![]() x=-
x=- ![]()
即: ![]() .
.
⊙C的极坐标方程为ρ=4cosθ+2sinθ.
可得:ρ2=4ρcosθ+2ρsinθ,
x2+y2=4x+2y
即:x2+y2﹣4x﹣2y=0,
故得直线l的普通方程为: ![]() ;⊙C的普通方程为:x2+y2﹣4x﹣2y=0
;⊙C的普通方程为:x2+y2﹣4x﹣2y=0
(2)解:由x2+y2﹣4x﹣2y=0,可知圆心为(2,1),半径r= ![]() ,
,
那么:圆心到直线的距离d= ![]() ,
,
∴|AB|=2 ![]()
故得直线l与圆⊙C交于A,B两点间的弦AB长为 ![]()
【解析】(1)将 ![]() 利用和差公式打开;根据x=ρcosθ,y=ρsinθ带入可得直线l和⊙C的普通方程.(2)利用圆截直线的弦长公式求|AB|即可
利用和差公式打开;根据x=ρcosθ,y=ρsinθ带入可得直线l和⊙C的普通方程.(2)利用圆截直线的弦长公式求|AB|即可


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC﹣A1B1C1中,AB⊥平面BB1C1C,∠BCC1= ![]() ,AB=BB1=2,BC=1,D为CC1中点.
,AB=BB1=2,BC=1,D为CC1中点. 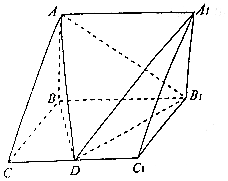
(1)求证:DB1⊥平面ABD;
(2)求二面角A﹣B1D﹣A1的平面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知{an}为等差数列,公差为d,且0<d<1,a5≠ ![]() (k∈Z),sin2a3+2sina5cosa5=sin2a7 , 函数f(x)=dsin(wx+4d)(w>0)满足:在
(k∈Z),sin2a3+2sina5cosa5=sin2a7 , 函数f(x)=dsin(wx+4d)(w>0)满足:在 ![]() 上单调且存在
上单调且存在 ![]() ,则w范围是 .
,则w范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知关于x的函数![]() ,其导函数
,其导函数![]() .
.
(1)如果函数![]() 在x=1处有极值
在x=1处有极值![]() 试确定b、c的值;
试确定b、c的值;
(2)设当![]() 时,函数
时,函数![]() 图象上任一点P处的切线斜率为k,若
图象上任一点P处的切线斜率为k,若![]() ,求实数b的取值范围.
,求实数b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P-ABC中,PA⊥AB,PA⊥BC,AB⊥BC,PA=AB=BC=2,D为线段AC的中点,E为线段PC上一点.

(1)求证:PA⊥BD;
(2)求证:平面BDE⊥平面PAC;
(3)当PA∥平面BDE时,求三棱锥E-BCD的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com