
【题目】(本小题满分12分)
已知函数![]() ,
,![]() 且
且![]() .
.
(Ⅰ)求![]() 的定义域;
的定义域;
(Ⅱ)判断![]() 的奇偶性并予以证明;
的奇偶性并予以证明;
(Ⅲ)当![]() 时,求使
时,求使![]() 的
的![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)解: ∵![]() ,
,
∴![]() 2分
2分
解得![]() . 4分
. 4分
故所求定义域为![]() . …………………………………………5分
. …………………………………………5分
(Ⅱ)由(Ⅰ)知![]() 的定义域为
的定义域为![]() ,
,
且![]() 7分
7分
![]()
![]() , 9分
, 9分
故![]() 为奇函数. ………………………………………………………………10分
为奇函数. ………………………………………………………………10分
(Ⅲ)因为f(x)>0,
所以loga(x+1)-loga(1-x)>0,即loga(x+1)>loga(1-x) 12分
因为当![]() 时,y=logax在(0,+)内是增函数,
时,y=logax在(0,+)内是增函数,
所以x+1>1-x,所以x>0, 13分
又![]() 的定义域为
的定义域为![]() ,所以
,所以![]() .
.
所以使![]() 的
的![]() 的取值范围是
的取值范围是![]() . ……………………14分
. ……………………14分
【解析】
解: (Ⅰ)![]() ,则
,则
![]() 解得
解得![]() .
.
故所求定义域为![]() .…………………………………4分
.…………………………………4分
(Ⅱ)由(Ⅰ)知![]() 的定义域为
的定义域为![]() ,
,
且![]()
![]()
![]() ,
,
故![]() 为奇函数. ………………………………………………9分
为奇函数. ………………………………………………9分
(Ⅲ)因为当![]() 时,
时,![]() 在定义域
在定义域![]() 内是增函数,
内是增函数,
所以![]() .
.
解得![]() .
.
所以使![]() 的
的![]() 的取值范围是
的取值范围是![]() .…………………12分
.…………………12分


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中数学 来源: 题型:
【题目】《数学九章》中对已知三角形三边长求三角形的面积的求法填补了我国传统数学的一个空白,与著名的海伦公式完全等价,由此可以看出我国古代已具有很高的数学水平,其求法是:“以小斜幂并大斜幂减中斜幂,余半之,自乘于上.以小斜幂乘大斜幂减上,余四约之,为实.一为从隔,开平方得积.”若把以上这段文字写成公式,即S= ![]() .现有周长为2
.现有周长为2 ![]() +
+ ![]() 的△ABC满足sinA:sinB:sinC=(
的△ABC满足sinA:sinB:sinC=( ![]() ﹣1):
﹣1): ![]() :(
:( ![]() +1),试用以上给出的公式求得△ABC的面积为( )
+1),试用以上给出的公式求得△ABC的面积为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆与双曲线有相同的焦点![]() ,
,![]() ,椭圆的一个短轴端点为
,椭圆的一个短轴端点为![]() ,直线
,直线![]() 与双曲线的一条渐近线平行,若椭圆于双曲线的离心率分别为
与双曲线的一条渐近线平行,若椭圆于双曲线的离心率分别为![]() ,
,![]() ,则
,则![]() 的最小值为__________.
的最小值为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以原点O为极点,x轴的正半轴为极轴建立极坐标系,直线l的方程为 ![]() ,⊙C的极坐标方程为ρ=4cosθ+2sinθ.
,⊙C的极坐标方程为ρ=4cosθ+2sinθ.
(1)求直线l和⊙C的普通方程;
(2)若直线l与圆⊙C交于A,B两点,求弦AB的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=2AD=4,E为边AB的中点,将△ADE沿直线DE翻转成△A1DE,构成四棱锥A1﹣BCDE,若M为线段A1C的中点,在翻转过程中有如下4个命题: ①MB∥平面A1DE;
②存在某个位置,使DE⊥A1C;
③存在某个位置,使A1D⊥CE;
④点A1在半径为 ![]() 的圆面上运动,
的圆面上运动,
其中正确的命题个数是( )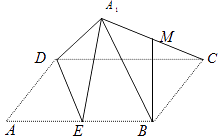
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题![]() :
: ![]() 表示双曲线,命题
表示双曲线,命题![]() :
: ![]() 表示椭圆。
表示椭圆。
(1)若命题![]() 与命题
与命题![]() 都为真命题,则
都为真命题,则![]() 是
是![]() 的什么条件?
的什么条件?
(请用简要过程说明是“充分不必要条件”、“必要不充分条件”、“充要条件”和“既不充分也不必要条件”中的哪一个)
(2)若![]() 为假命题,且
为假命题,且![]() 为真命题,求实数
为真命题,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 经过点
经过点 ,离心率为
,离心率为![]() ,动点M(2,t)(
,动点M(2,t)(![]() ).
).
(1)求椭圆的标准方程;
(2)求以OM为直径且截直线![]() 所得的弦长为2的圆的方程;
所得的弦长为2的圆的方程;
(3)设F是椭圆的右焦点,过点F作OM的垂线与以OM为直径的圆交于点N,证明线段ON的长为定值,并求出这个定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() :
: ![]() (其中
(其中![]() 为圆心)上的每一点横坐标不变,纵坐标变为原来的一半,得到曲线
为圆心)上的每一点横坐标不变,纵坐标变为原来的一半,得到曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)若点![]() 为曲线
为曲线![]() 上一点,过点
上一点,过点![]() 作曲线
作曲线![]() 的切线交圆
的切线交圆![]() 于不同的两点
于不同的两点![]() (其中
(其中![]() 在
在![]() 的右侧),已知点
的右侧),已知点![]() .求四边形
.求四边形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com