
【题目】已知圆![]() :
: ![]() (其中
(其中![]() 为圆心)上的每一点横坐标不变,纵坐标变为原来的一半,得到曲线
为圆心)上的每一点横坐标不变,纵坐标变为原来的一半,得到曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)若点![]() 为曲线
为曲线![]() 上一点,过点
上一点,过点![]() 作曲线
作曲线![]() 的切线交圆
的切线交圆![]() 于不同的两点
于不同的两点![]() (其中
(其中![]() 在
在![]() 的右侧),已知点
的右侧),已知点![]() .求四边形
.求四边形![]() 面积的最大值.
面积的最大值.
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,以原点O为极点,x轴正半轴为极轴建立极坐标系.若曲线C的极坐标方程为ρcos2θ﹣4sinθ=0,P点的极坐标为 ![]() ,在平面直角坐标系中,直线l经过点P,斜率为
,在平面直角坐标系中,直线l经过点P,斜率为 ![]()
(Ⅰ)写出曲线C的直角坐标方程和直线l的参数方程;
(Ⅱ)设直线l与曲线C相交于A,B两点,求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,多面体EF﹣ABCD中,ABCD是正方形,AC、BD相交于O,EF∥AC,点E在AC上的射影恰好是线段AO的中点.
(Ⅰ)求证:BD⊥平面ACF;
(Ⅱ)若直线AE与平面ABCD所成的角为60°,求平面DEF与平面ABCD所成角的正弦值.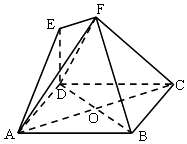
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P-ABC中,PA⊥AB,PA⊥BC,AB⊥BC,PA=AB=BC=2,D为线段AC的中点,E为线段PC上一点.

(1)求证:PA⊥BD;
(2)求证:平面BDE⊥平面PAC;
(3)当PA∥平面BDE时,求三棱锥E-BCD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图下图①,等边三角形ABC的边长为2a,CD是AB边上的高,E,F分别是AC和BC边上的点,且满足![]() =k,现将△ABC沿CD翻折成直二面角ADCB,如图下图②.
=k,现将△ABC沿CD翻折成直二面角ADCB,如图下图②.
(1)试判断翻折后直线AB与平面DEF的位置关系,并说明理由;
(2)求二面角BACD的正切值.
① ②
②
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】农科院的专家为了了解新培育的甲、乙两种麦苗的长势情况,从甲、乙两种麦苗的试验田中各抽取6株麦苗测量麦苗的株高,数据如下:(单位:cm)
甲:9,10,11,12,10,20
乙:8,14,13,10,12,21.
(1)在给出的方框内绘出所抽取的甲、乙两种麦苗株高的茎叶图;
(2)分别计算所抽取的甲、乙两种麦苗株高的平均数与方差,并由此判断甲、乙两种麦苗的长势情况.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com