
| A. | $({0,\frac{{2-\sqrt{2}}}{2}})$ | B. | $({2-\sqrt{2},1})$ | C. | $({1,2+\sqrt{2}}]$ | D. | $({-∞,2+\sqrt{2}}]$ |
分析 利用奇偶函数的定义可判定f(x)=x+sinx为奇函数,再利用导数法克判断出f(x)=x+sinx为增函数,分离参数a,可得g(θ)=$\frac{1}{1-sinθ}$在区间$(\frac{π}{4},\frac{π}{2})$上单调递增,从而得到a≤g($\frac{π}{4}$)=2+$\sqrt{2}$,得到答案.
解答 解:∵f(x)=x+sinx,
∴f(-x)=-x+sin(-x)=-x-sinx=-f(x),
∴函数f(x)=x+sinx为奇函数,
又f′(x)=1+cosx≥0,
∴函数f(x)=x+sinx为增函数,
∴f(asinθ)+f(1-a)>0恒成立?f(asinθ)>-f(1-a)=f(a-1),
∴asinθ>a-1,
∵当$θ∈({\frac{π}{4},\frac{π}{2}})$时,sinθ>0,
∴a<$\frac{1}{1-sinθ}$($\frac{π}{4}$<θ<$\frac{π}{2}$)恒成立,∵g(θ)=$\frac{1}{1-sinθ}$在区间$(\frac{π}{4},\frac{π}{2})$上单调递增,
∴a≤g($\frac{π}{4}$)=$\frac{1}{1-\frac{\sqrt{2}}{2}}$=2+$\sqrt{2}$,
∴实数a的取值范围是(-∞,2+$\sqrt{2}$],
故选:D.
点评 本题考查函数恒成立问题,考查函数奇偶性与单调性的判定及应用,分离参数a是关键,考查等价转化思想与运算求解能力,属于难题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
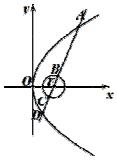 如图,已知抛物线y2=4x的焦点为F,直线l过F且依次交抛物线及圆${(x-1)^2}+{y^2}=\frac{1}{4}$于点A,B,C,D四点,则4|AB|+9|CD|的最小值为$\frac{37}{2}$.
如图,已知抛物线y2=4x的焦点为F,直线l过F且依次交抛物线及圆${(x-1)^2}+{y^2}=\frac{1}{4}$于点A,B,C,D四点,则4|AB|+9|CD|的最小值为$\frac{37}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com