
【题目】已知函数![]() ,其中
,其中![]() .
.
(1)若![]() ,求函数
,求函数![]() 的单调区间;
的单调区间;
(2)若关于![]() 的不等式
的不等式![]() 对任意的实数
对任意的实数![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)若函数![]() 有
有![]() 个不同的零点,求实数
个不同的零点,求实数![]() 的取值范围.
的取值范围.
【答案】(1)单调减区间是![]() ,单调增区间是
,单调增区间是![]() ,(2)
,(2)![]() (3)
(3)![]()
【解析】
(1)化简得到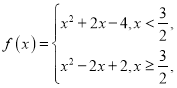 ,分别计算单调性得到答案.
,分别计算单调性得到答案.
(2)化简得到![]() 恒成立,计算函数
恒成立,计算函数![]() 的最大值得到答案.
的最大值得到答案.
(3)化简得到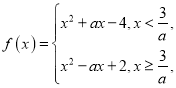 ,确定
,确定![]() 在
在![]() 和
和![]() 上都各有
上都各有![]() 个不同的零点,计算得到答案.
个不同的零点,计算得到答案.
(1)当![]() 时,
时,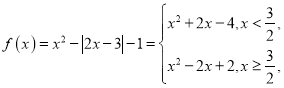
当![]() 时,
时,![]() ,
,
所以![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递减.
上单调递减.
当![]() 时,
时,![]() ,
,
所以![]() 在
在![]() 上单调递增.
上单调递增.
因为函数![]() 的图象在
的图象在![]() 上不间断,
上不间断,
所以![]() 的单调减区间是
的单调减区间是![]() ,单调增区间是
,单调增区间是![]() .
.
(2)![]() 对任意
对任意![]() 恒成立.
恒成立.
因为![]() ,
,![]() ,所以
,所以![]() ,
,
故不等式可化为![]() ,即
,即![]() ,
,
所以问题转化为不等式![]() 对任意
对任意![]() 恒成立.
恒成立.
又![]() 在
在![]() 上单调递减,
上单调递减,
所以![]() ,
,
所以![]() .
.
(3)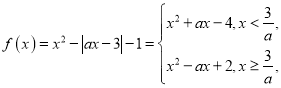 ,其中
,其中![]() .
.
显然,当![]() 时,
时,![]() 至多有
至多有![]() 个不同的零点,且当
个不同的零点,且当![]() 时,
时,
![]() 至多有
至多有![]() 个不同的零点,
个不同的零点,
又![]() 有
有![]() 个不同的零点,
个不同的零点,
所以![]() 在
在![]() 和
和![]() 上都各有
上都各有![]() 个不同的零点,
个不同的零点,
所以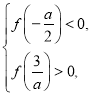 且
且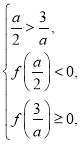 即
即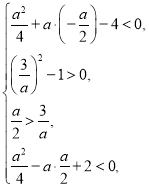
又![]() ,解得
,解得![]() ,
,
所以实数![]() 的取值范围是
的取值范围是![]() .
.


科目:高中数学 来源: 题型:
【题目】已知以点C![]() (t∈R,t≠0)为圆心的圆与x轴交于点O和点A,与y轴交于点O和点B,其中O为原点.
(t∈R,t≠0)为圆心的圆与x轴交于点O和点A,与y轴交于点O和点B,其中O为原点.
(1)求证:△OAB的面积为定值;
(2)设直线y=-2x+4与圆C交于点M,N,若OM=ON,求圆C的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正三棱柱![]() (底面为正三角形,侧棱和底面垂直)的所有棱长都为2,
(底面为正三角形,侧棱和底面垂直)的所有棱长都为2,![]() 为
为![]() 的中点,O为
的中点,O为![]() 中点.
中点.
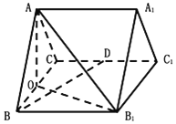
(1)求证:![]() 平面
平面![]() .
.
(2)求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数![]() ,总存在实数
,总存在实数![]() ,使
,使![]() 成立,则称
成立,则称![]() 为
为![]() 关于参数
关于参数![]() 的不动点.
的不动点.
(1)当![]() ,
,![]() 时,求
时,求![]() 关于参数
关于参数![]() 的不动点;
的不动点;
(2)若对任意实数![]() ,函数
,函数![]() 恒有关于参数
恒有关于参数![]() 两个不动点,求
两个不动点,求![]() 的取值范围;
的取值范围;
(3)当![]() ,
,![]() 时,函数
时,函数![]() 在
在![]() 上存在两个关于参数
上存在两个关于参数![]() 的不动点,试求参数
的不动点,试求参数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司欲生产一款迎春工艺品回馈消费者,工艺品的平面设计如图所示,该工艺品由直角![]() 和以
和以![]() 为直径的半圆拼接而成,点
为直径的半圆拼接而成,点![]() 为半圈上一点(异于
为半圈上一点(异于![]() ,
,![]() ),点
),点![]() 在线段
在线段![]() 上,且满足
上,且满足![]() .已知
.已知![]() ,
,![]() ,设
,设![]() .
.

(1)为了使工艺礼品达到最佳观赏效果,需满足![]() ,且
,且![]() 达到最大.当
达到最大.当![]() 为何值时,工艺礼品达到最佳观赏效果;
为何值时,工艺礼品达到最佳观赏效果;
(2)为了工艺礼品达到最佳稳定性便于收藏,需满足![]() ,且
,且![]() 达到最大.当
达到最大.当![]() 为何值时,
为何值时,![]() 取得最大值,并求该最大值.
取得最大值,并求该最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一款击鼓小游戏的规则如下:每盘游戏都需要击鼓三次,每次击鼓要么出现一次音乐,要么不出现音乐;每盘游戏击鼓三次后,出现一次音乐获得10分,出现两次音乐获得20分,出现三次音乐获得100分,没有出现音乐则扣除200分(即获得![]() 分).设每次击鼓出现音乐的概率为
分).设每次击鼓出现音乐的概率为![]() ,且各次击鼓出现音乐相互独立.
,且各次击鼓出现音乐相互独立.
(1)设每盘游戏获得的分数为![]() ,求
,求![]() 的分布列;
的分布列;
(2)玩三盘游戏,至少有一盘出现音乐的概率是多少?
(3)玩过这款游戏的许多人都发现,若干盘游戏后,与最初的分数相比,分数没有增加反而减少了.请运用概率统计的相关知识分析分数减少的原因.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某研究性学习小组对春季昼夜温差大小与某花卉种子发芽多少之间的关系进行研究,他们分别记录了3月1日至3月5日的每天昼夜温差与实验室每天每100颗种子浸泡后的发芽数,得到如下资料:
日期 | 3月1日 | 3月2日 | 3月3日 | 3月4日 | 3月5日 |
温差 | 10 | 11 | 13 | 12 | 9 |
发芽数 | 23 | 25 | 30 | 26 | 16 |
(1)从3月1日至3月5日中任选2天,记发芽的种子数分别为![]() ,
,![]() ,求事件“
,求事件“![]() ”的概率;
”的概率;
(2)该小组发现种子的发芽数![]() (颗)与昼夜温差
(颗)与昼夜温差![]() (℃)呈线性相关关系,试求:线性回归方程
(℃)呈线性相关关系,试求:线性回归方程![]() .
.
(参考公式:线性回归方程![]() 中系数计算公式
中系数计算公式 ,
,![]() .其中
.其中![]() ,
,![]() 表示样本均值.
表示样本均值.
参考数据:![]() ;
;![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某射击运动员每次击中目标的概率都是![]() ,现采用随机模拟的方法估计该运动员射击
,现采用随机模拟的方法估计该运动员射击![]() 次至多击中
次至多击中![]() 次的概率:先由计算器产生
次的概率:先由计算器产生![]() 到
到![]() 之间取整数值的随机数,指定
之间取整数值的随机数,指定![]() 、
、![]() 表示没有击中目标,
表示没有击中目标,![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 表示击中目标,因为射击
表示击中目标,因为射击![]() 次,故以每
次,故以每![]() 个随机数为一组,代表射击
个随机数为一组,代表射击![]() 次的结果.经随机模拟产生了如下
次的结果.经随机模拟产生了如下![]() 组随机数:
组随机数:
5727 0293 7140 9857 0347 4373 8636 9647 1417 4698
0371 6233 2616 8045 6011 3661 9597 7424 6710 4281
据此估计,射击运动员射击4次至多击中3次的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆W:![]() (a>b>0)的离心率
(a>b>0)的离心率![]() ,其右顶点A(2,0),直线l过点B(1,0)且与椭圆交于C,D两点.
,其右顶点A(2,0),直线l过点B(1,0)且与椭圆交于C,D两点.
(Ⅰ)求椭圆W的标准方程;
(Ⅱ)判断点A与以CD为直径的圆的位置关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com