
已知三棱锥P-ABC是正三棱锥,求证:
(1)它的各个侧面与底面所成的角相等;
(2)正三棱锥底面积与侧面积S之比是各个侧面与底面所成角的余弦值.
|
证明:因三棱锥P-ABC是正三棱锥,故顶点P在底面上的射影O是底面正△ABC的中心,连结AO、BO、CO,并延长分别交对边于D、E、F三点.
(1)∵△ABC是正三角形, ∴AD⊥BC,OD=OE=OF. 又∵PO⊥BC,∴BC⊥面PAD.∴BC⊥PD. ∴∠PDA就是侧面PBC与底面ABC所成二面角的平面角. 同理,∠PEB、∠PFC分别是另两个侧面与底面所成二面角的平面角. 可证得Rt△PFO≌Rt△PDO≌Rt△PEO, ∴∠PEB=∠PFC=∠PDA,即结论(1)成立. (2)由∠PEB=∠PFC=∠PDA, ∴cos∠PEB=cos∠PFC=cos∠PDA, 即cos∠PEB= ∴cos∠PEB= 解析:(1)本题首先要作出各个侧面与底面所成的二面角.以侧面PBC为例,取BC的中点D,连结PD、AD,则易证BC⊥PD,BC⊥AD.从而∠PDA就是侧面PBC与底面ABC所成二面角的平面角.(2)注意侧面△PBC与其在底面上的投影△OBC是底边相等的三角形,且它们的高同在Rt△PDO中,且比例恰为侧面与底面所成角的余弦值,从而易得其面积的比例关系. |


科目:高中数学 来源:2013届浙江省宁波万里国际学校高二下期中理科数学试卷(解析版) 题型:解答题
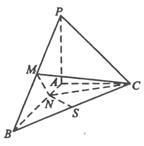
(本题满分14分)已知三棱锥P-ABC中,PA⊥平面ABC,AB⊥AC,PA=AC=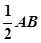 ,N为AB上一点,AB=4AN, M,S分别为PB,BC的中点.
,N为AB上一点,AB=4AN, M,S分别为PB,BC的中点.
(Ⅰ)证明:CM⊥SN;
(Ⅱ)求SN与平面CMN所成角的大小.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年甘肃省高三百题集理科数学试卷(解析版)(四) 题型:解答题
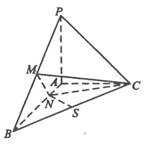
已知三棱锥P-ABC中,PA⊥ABC,AB⊥AC,PA=AC=½AB,N为AB上一点,AB=4AN,M,S分别为PB,BC的中点.
(Ⅰ)证明:CM⊥SN;
(Ⅱ)求SN与平面CMN所成角的大小.
查看答案和解析>>
科目:高中数学 来源:2010年普通高等学校招生全国统一考试(辽宁卷)理科数学 题型:解答题
已知三棱锥P-ABC中,PA⊥ABC,AB⊥AC,PA=AC=½AB,N为AB上一点,AB=4AN,M,S分别为PB,BC的中点.
(Ⅰ)证明:CM⊥SN;
(Ⅱ)求SN与平面CMN所成角的大小.
查看答案和解析>>
科目:高中数学 来源:2010-2011年重庆市高二下学期第二次月考理科数学 题型:选择题
已知三棱锥P-ABC中,PA、PB、PC两两垂直,PA=PB=2PC=2a,且三棱锥外接球的表面积为S=9π,则实数a的值为( )
A. B.2 C. 1 D.
查看答案和解析>>
科目:高中数学 来源:2010-2011年重庆市高二下学期第二次月考文科数学 题型:选择题
已知三棱锥P-ABC中,PA、PB、PC两两垂直,PA=PB=2PC=2a,且三棱锥外接球的表面积为S=9π,则实数a的值为( )
A. B.2 C. D. 1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com