
【题目】已知函数 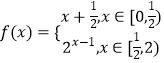 ,若存在x1 , x2 , 当0≤x1<x2<2时,f(x1)=f(x2),则x1f(x2)﹣f(x2)的取值范围为( )
,若存在x1 , x2 , 当0≤x1<x2<2时,f(x1)=f(x2),则x1f(x2)﹣f(x2)的取值范围为( )
A.![]()
B.![]()
C.![]()
D.![]()
【答案】B
【解析】解:作出函数的图象:
∵存在x1 , x2 , 当0≤x1<x2<2时,f(x1)=f(x2)
∴0≤x1< ![]() ,
,
∵x+ ![]() 在[0,
在[0, ![]() )上的最小值为
)上的最小值为 ![]() ;
;
2x﹣1在[ ![]() ,2)的最小值为
,2)的最小值为 ![]() ,
,
∴x1+ ![]() ≥
≥ ![]() ,x1≥
,x1≥ ![]() ,
,
∴ ![]() ≤x1<
≤x1< ![]() .
.
∵f(x1)=x1+ ![]() ,f(x1)=f(x2)
,f(x1)=f(x2)
∴x1f(x2)﹣f(x2)=x1f(x1)﹣f(x1)2
= ![]() ﹣(x1+
﹣(x1+ ![]() )=x12﹣
)=x12﹣ ![]() x1﹣
x1﹣ ![]() ,
,
设y=x12﹣ ![]() x1﹣
x1﹣ ![]() =(x1﹣
=(x1﹣ ![]() )2﹣
)2﹣ ![]() ,(
,( ![]() ≤x1<
≤x1< ![]() ),
),
则对应抛物线的对称轴为x= ![]() ,
,
∴当x= ![]() 时,y=﹣
时,y=﹣ ![]() ,
,
当x= ![]() 时,y=
时,y= ![]() ,
,
即x1f(x2)﹣f(x2)的取值范围为[﹣ ![]() ,
, ![]() ).
).
故选:B.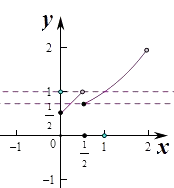


 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案科目:高中数学 来源: 题型:
【题目】已知![]() ,设
,设![]() ,
,![]() ,
,![]() (
(![]() ,
,![]() 为常数).
为常数).
(1)求![]() 的最小值及相应的
的最小值及相应的![]() 的值;
的值;
(2)设![]() ,若
,若![]() ,求
,求![]() 的取值范围;
的取值范围;
(3)若对任意![]() ,以
,以![]() 、
、![]() 、
、![]() 为三边长总能构成三角形,求
为三边长总能构成三角形,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知四棱锥S﹣ABCD,SB⊥AD,侧面SAD是边长为4的等边三角形,底面ABCD为菱形,侧面SAD与底面ABCD所成的二面角为120°.
(1)求点S到平面ABCD的距离;
(2)若E为SC的中点,求二面角A﹣DE﹣C的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某海关对同时从![]() 三个不同地区进口的某种商品进行随机抽样检测,已知从
三个不同地区进口的某种商品进行随机抽样检测,已知从![]() 三个地区抽取的商品件数分别是50,150,100.检测人员再用分层抽样的方法从海关抽样的这些商品中随机抽取6件样品进行检测.
三个地区抽取的商品件数分别是50,150,100.检测人员再用分层抽样的方法从海关抽样的这些商品中随机抽取6件样品进行检测.
(1)求这6件样品中,来自![]() 各地区商品的数量;
各地区商品的数量;
(2)若在这6件样品中随机抽取2件送往另一机构进行进一步检测,求这2件样品来自相同地区的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在多面体![]() 中,
中, ![]() 与
与![]() 均为边长为2的正方形,
均为边长为2的正方形, ![]() 为等腰直角三角形,
为等腰直角三角形, ![]() ,且平面
,且平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() .
.
(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某汽配厂生产某种零件,每个零件的出厂单价为60元,为了鼓励更多销售商订购,该厂决定当一次订购超过100个时,每多订购一个,订购的全部零件的出厂单价就降低![]() 元,但实际出厂单价不低于51元.
元,但实际出厂单价不低于51元.
![]() 当一次订购量最少为多少时,零件的实际出厂单价恰好为51元?
当一次订购量最少为多少时,零件的实际出厂单价恰好为51元?
![]() 设一次订购量为x个,零件的实际出厂单价为p元,写出函数
设一次订购量为x个,零件的实际出厂单价为p元,写出函数![]() 的表达式.
的表达式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,以原点为极点,x轴的正半轴为极轴建立极坐标系,已知曲线C:ρsin2θ=2acosθ(a>0),直线l的参数方程为  (t为参数),l与C分别交于M,N,P(﹣2,﹣4).
(t为参数),l与C分别交于M,N,P(﹣2,﹣4).
(1)写出C的平面直角坐标系方程和l的普通方程;
(2)已知|PM|,|MN|,|PN|成等比数列,求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,我国许多省市雾霾天气频发,为增强市民的环境保护意识,某市面向全市征召n名义务宣传志愿者,成立环境保护宣传组织![]() 现把该组织的成员按年龄分成5组:第1组
现把该组织的成员按年龄分成5组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,得到的频率分布直方图如图所示,已知第2组有70人.
,得到的频率分布直方图如图所示,已知第2组有70人.
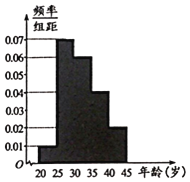
(1)求该组织的人数.
(2)若从第3,4,5组中用分层抽样的方法抽取6名志愿者参加某社区的宣传活动,然后在这6名志愿者中随机抽取2名志愿者介绍宣传经验,求第3组至少有一名志愿者被抽中的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com