已知集合A={x|x2+px+q=0},B={x|qx2+px+1=0}.同时满足:①A∩B≠∅,②A∩CuB={-2},其中p、q均为不等于零的实数,求p、q的值.
解:设x
0∈A,则x
0≠0,否则将有q=0与题设矛盾.
于是由
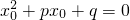
,两边同除以
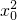
,得
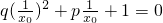
,
知
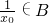
,故集合A、B中的元素互为倒数.
由①知存在x
0∈A,
使得
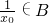
,且
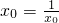
,
得x
0=1或x
0=-1.
由②知A={1,-2}或A={-1,-2}.
若A={1,-2},
则
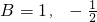
,有
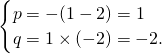
同理,若A={-1,-2},则
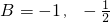
,
得p=3,q=2.
综上,p=1,q=-2或p=3,q=2.
分析:条件①是说集合A、B有相同的元素,条件②是说-2∈A但-2∉B,A、B是两个方程的解集,方程x
2+px+q=0和qx
2+px+1=0的根的关系的确定是该题的突破口,求p、q的值.
点评:本题考查了二次函数的性质及方程的根与系数的关系,是一道中档题,考查了分类讨论的思想,考查的知识点比较全面;

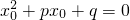 ,两边同除以
,两边同除以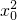 ,得
,得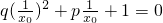 ,
,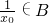 ,故集合A、B中的元素互为倒数.
,故集合A、B中的元素互为倒数.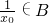 ,且
,且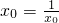 ,
,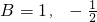 ,有
,有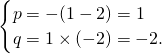
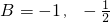 ,
,
